Задача
На стороне BC остроугольного треугольника ABC (AB≠BC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=49, MD=42, H — точка пересечения высот треугольника ABC.
Найти AH.

Задача
На стороне BC остроугольного треугольника ABC (AB≠BC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=49, MD=42, H — точка пересечения высот треугольника ABC.
Найти AH.
Задача
В треугольнике ABC известны длины сторон AB=28, AC=56, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найти CD.
Задача
В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:4, считая от точки B. Найти радиус окружности, описанной около треугольника ABC, если BC=12.
Решение:
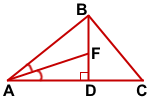 Пусть биссектриса угла A пересекает высоту BD треугольника ABC в точке F.
Пусть биссектриса угла A пересекает высоту BD треугольника ABC в точке F.
По условию, BF:FD=5:4.
Рассмотрим треугольник ABD, ∠ADB=90°.
Задача
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=5 и MB=10. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найти CD.
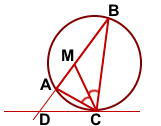 Дано: ΔABC вписан в окр.(O;R),
Дано: ΔABC вписан в окр.(O;R),
CM — биссектриса ∠ACB, CD — касательная к окр.(O;R),
AM=5, MB=10, CD∩AB=D
Найти: CD
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Задача.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Если сторона треугольника равна радиусу описанной окружности, то что можно сказать о свойствах такого треугольника?
Как найти уравнение окружности, симметричной данной?
Симметричные окружности имеют равные радиусы. Следовательно, остаётся найти координаты центра симметричной окружности (как точки, симметричной данной).
Примеры.
1) Окружность задана уравнением (x-3)²+(y+2)²=16. Составить уравнение окружности, симметричной данной относительно точки (7; 10).