Утверждение
Если две медианы треугольника равны, то этот треугольник — равнобедренный.
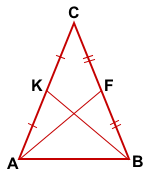 Дано: ΔABC,
Дано: ΔABC,
AF, BK — медианы,
AF=BK
Доказать: ΔABC — равнобедренный

Утверждение
Если две медианы треугольника равны, то этот треугольник — равнобедренный.
 Дано: ΔABC,
Дано: ΔABC,
AF, BK — медианы,
AF=BK
Доказать: ΔABC — равнобедренный
Теорема (Штейнера-Лемуса)
Если в треугольнике две биссектрисы равны, то этот треугольник — равнобедренный.
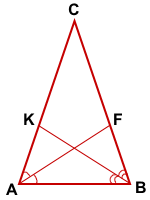 Дано:
Дано:
ΔABC,
AF, BK — биссектрисы ΔABC,
AF=BK
Доказать: ΔABC — равнобедренный
Доказательство:
Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.
I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.
Утверждение 1
Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
Задача
В равнобедренную трапецию, периметр которой 220, а площадь равна 2420, можно вписать окружность.
Найти расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
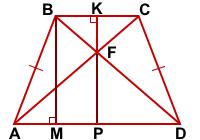 Дано: ABCD — трапеция,
Дано: ABCD — трапеция,
AD || BC, AB=CD,
PABCD=220, SABCD=2420,
AC∩BC=F, FK⊥BC
Найти: FK
Задача
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K.
Найти площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 10.
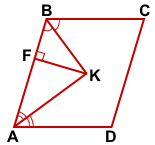 Дано: ABCD — параллелограмм,
Дано: ABCD — параллелограмм,
AK, BK — биссектрисы углов BAD и ABC,
AK∩BK=K, KF⊥AB,
KF=10, BC=19
Найти: SABCD
Задача
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8.
Найти стороны треугольника ABC.
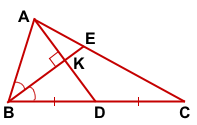 Дано: ΔABC,
Дано: ΔABC,
AD — медиана, BE — биссектриса,
AD=BE=8, AD⊥BE
Найти: AB, BC, AC
Задача
Боковые стороны AB и CD трапеции ABCD равны соответственно16 и 34, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB.Найти площадь трапеции.
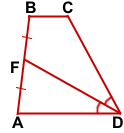 Дано: ABCD — трапеция, AD || BC, BC=2,
Дано: ABCD — трапеция, AD || BC, BC=2,
AB=16, CD=34, DF — биссектриса ∠ADC, F — середина AB
Найти: SABCD
Решение: