Биссектрисы углов A и B параллелограмма пересекаются в точке K

Задача

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K.

Найти площадь параллелограмма, если BC=19,  а расстояние от точки K до стороны AB равно 10.

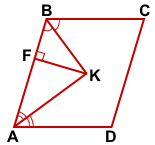Дано: ABCD — параллелограмм,

AK, BK — биссектрисы углов BAD и ABC,

AK∩BK=K, KF⊥AB,

KF=10, BC=19

Найти: S_ABCD

Решение:

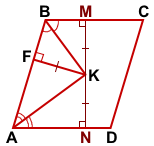Проведём через точку K высоту параллелограмма MN.

Так как любая точка биссектрисы угла равноудалена от его сторон, то

KM=KF=10, KN=KF=10.

MN=KM+KN=20.

По формуле S=a∙h

площадь параллелограмма S_ABCD=BC∙MN, S_ABCD=19∙10=190.

Ответ: 190.

 

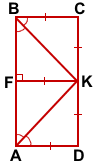
Замечание

В частном случае, если BC=KF, ABCD — прямоугольник, и K — середина CD.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Значит отрезок, который BK отсекает на стороне CD, равен BC.

Расстояние от K до BC равно длине перпендикуляра, опущенного из точки K на прямую BC.

Из данной точки к данной прямой можно провести только один перпендикуляр. Значит CK⊥BC. Следовательно, ABCD — прямоугольник.