Замечательное свойство трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.
Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.
Сформулируем это свойство иначе:
Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.
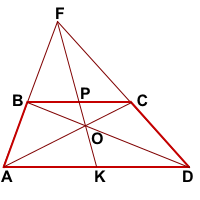 Дано:
Дано:
ABCD- трапеция, AD||BC,
AB∩CD=F, AC∩BD=O,
FO∩AD=K, FO∩BC=P
Доказать: K- середина AD,
P- середина BC
Доказательство:
…Continue reading

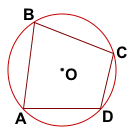 Дано: ABCD вписан в окр. (O; R)
Дано: ABCD вписан в окр. (O; R)
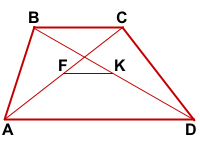 Дано: ABCD — трапеция, AD||BC,
Дано: ABCD — трапеция, AD||BC, Дано:
Дано: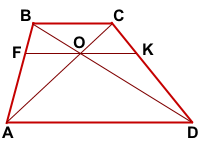 Дано: ABCD — трапеция, AD||BC,
Дано: ABCD — трапеция, AD||BC,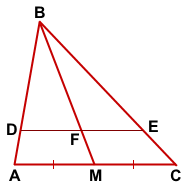 Дано: ΔABC,
Дано: ΔABC,