Признак принадлежности четырёх точек одной окружности
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.
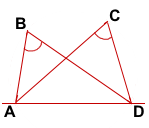
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,
∠ABD=∠ACD
Доказать: точки A, B, C, D лежат на одной окружности
Доказательство:
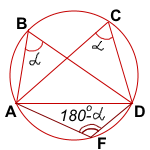 Обозначим ∠ABD=∠ACD=α.
Обозначим ∠ABD=∠ACD=α.
Опишем около треугольника ABD окружность.
Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.
Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:
∠ABD+∠AFD=180°.
Отсюда ∠AFD=180°-∠ABD=180°-α.
Рассмотрим четырехугольник ACDF.
∠ACD+∠AFD=α+180°-α=180°.
Отсюда следует, что четырёхугольник ABDF — вписанный.
Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.
Что и требовалось доказать.
