Отрезок через точку пересечения диагоналей трапеции |

Утверждение 1

Отрезок, проходящий через точку пересечения диагоналей трапеции параллельно основаниям, делится этой точкой пополам.

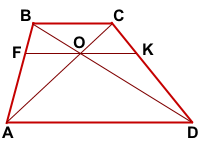otrezok-cherez-tochku-peresecheniya-diagonalej-trapecii Дано: ABCD — трапеция, AD||BC,

AC∩BD=O, F∈AB, K∈CD,

FK||AD, O∈FK

Доказать: O — середина FK.

Доказательство:

1-й способ доказательства

Рассмотрим треугольники AOD и COB.

∠AOD=∠COB (как вертикальные),

∠DAO=∠BCO (как внутренние накрест лежащие при AD||BC и секущей AC).

Значит, треугольники AOD и COB подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$\frac{{AD}}{{BC}} = \frac{{AO}}{{OC}} = \frac{{DO}}{{BO}}.$

Обозначим AD=a, BC=b, тогда

$\frac{a}{b} = \frac{{AO}}{{OC}} = \frac{{DO}}{{BO}}.$

Рассмотрим треугольники ABC и FBO.

∠B — общий,

∠BAD=∠BFO (как внутренние накрест лежащие при AD||FK и секущей AB).

Значит, треугольники ABC и FBO подобны (по двум углам).

Следовательно,

$\frac{{AD}}{{FO}} = \frac{{BD}}{{BO}}.$

$\frac{{AD}}{{FO}} = \frac{{BD}}{{BO}} = \frac{{DO + BO}}{{BO}} = \frac{{DO}}{{BO}} + \frac{{BO}}{{BO}} = \frac{{DO}}{{BO}} + 1,$

$\frac{a}{{FO}} = \frac{a}{b} + 1, \Rightarrow \frac{a}{{FO}} = \frac{{a + b}}{b},$

откуда

$FO = \frac{{ab}}{{a + b}}.$

Аналогично, треугольники ACD и ОСК подобны и

$\frac{{AD}}{{OK}} = \frac{{AC}}{{OC}}.$

Отсюда

$\frac{{AD}}{{OK}} = \frac{{AO + OC}}{{OC}} = \frac{{AO}}{{OC}} + \frac{{OC}}{{OC}} = \frac{{AO}}{{OC}} + 1,$

$\frac{a}{{OK}} = \frac{a}{b} + 1, \Rightarrow \frac{a}{{OK}} = \frac{{a + b}}{b},$

$OK = \frac{{ab}}{{a + b}}.$

Следовательно, FO=OK, то есть точка O — середина отрезка FK.

Что и требовалось доказать.

В ходе доказательства выразили длины FO и OK через длины оснований. Отсюда можно получить формулу для нахождения длины FK.

Утверждение 2

Длина отрезка, проходящего через точку пересечения диагоналей трапеции параллельно её основаниям, равна частному от деления удвоенного произведения длин оснований на сумму оснований:

$FK = \frac{{2 \cdot AD \cdot BC}}{{AD + BC}},$

или

$FK = \frac{{2ab}}{{a + b}}.$

Определение.

Средним гармоническим нескольких положительных чисел называют число, обратное среднему арифметическому чисел, обратных данным.

Для чисел x₁, x₂,…, x_n среднее гармоническое

$h = \frac{1}{{(\frac{1}{{x_1 }} + \frac{1}{{x_2 }} + ... + \frac{1}{{x_n }}):n}} = \frac{n}{{\frac{1}{{x_1 }} + \frac{1}{{x_2 }} + ... + \frac{1}{{x_n }}}}.$

Так как

$\frac{1}{{(\frac{1}{a} + \frac{1}{b}):2}} = \frac{1}{{\frac{{b + a}}{{ab}}:2}} = \frac{{2ab}}{{a + b}},$

Длина отрезка, проходящего через точку пересечения диагоналей трапеции параллельно её основаниям, равна среднему гармоническому длин оснований.

2-й способ доказательства

Доказать, что что медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.
Доказать замечательное свойство трапеции: точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.

Тогда в треугольнике, две вершины которого — концы большего основания трапеции, а третья — точка пересечения продолжения боковых сторон трапеции, отрезок, соединяющий точку пересечения продолжения боковых сторон трапеции с серединой большего основания — медиана. А значит, она пополам делит отрезок, проходящий через точку пересечения диагоналей трапеции параллельно её основаниям.

Отрезок, проходящий через точку пересечения диагоналей трапеции

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики