Замечательное свойство трапеции |

Замечательное свойство трапеции

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.

Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.

Сформулируем это свойство иначе:

Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.

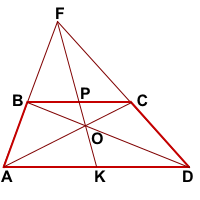zamechatelnoe-svojstvo-trapecii Дано:

ABCD- трапеция, AD||BC,

AB∩CD=F, AC∩BD=O,

FO∩AD=K, FO∩BC=P

Доказать: K- середина AD,

P- середина BC

Доказательство:

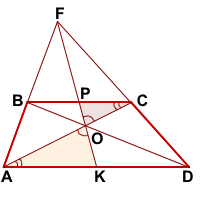serediny-osnovanij-trapecii-i-tochka-peresecheniya-diagonalej Рассмотрим треугольники AOK и COP.

∠AOK=∠COP (как вертикальные),

∠OAK=∠OCP (как внутренние накрест лежащие при AD||BC и секущей AC).

Значит, треугольники AOK и COP подобны (по двум углам).

Следовательно,

$\frac{{AK}}{{CP}} = \frac{{KO}}{{PO}}.$

Аналогично, треугольники DOK и BOP подобны и

$\frac{{DK}}{{BP}} = \frac{{KO}}{{PO}}.$

Так как правые части этих равенств равны, то левые также равны:

$\frac{{AK}}{{CP}} = \frac{{DK}}{{BP}}, \Rightarrow AK = \frac{{CP \cdot DK}}{{BP}},CP = \frac{{BP \cdot AK}}{{DK}}.$

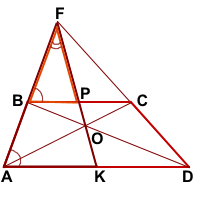serediny-osnovanij-trapecii-tochka-peresecheniya Рассмотрим треугольники AFK и BFP.

∠F- общий,

∠KAF=∠PBF (как соответственные при AD||BC и секущей AF).

Следовательно, треугольники AFK и BFP подобны (по двум углам).

Отсюда,

$\frac{{AK}}{{BP}} = \frac{{FK}}{{FP}}.$

Аналогично, треугольники DFK и CFP подобны и

$\frac{{DK}}{{CP}} = \frac{{FK}}{{FP}}.$

Правые части равенств равны, приравниваем левые части:

$\frac{{AK}}{{BP}} = \frac{{DK}}{{CP}}, \Rightarrow AK = \frac{{BP \cdot DK}}{{CP}},CP = \frac{{BP \cdot DK}}{{AK}}.$

Так как

$AK = \frac{{CP \cdot DK}}{{BP}},AK = \frac{{BP \cdot DK}}{{CP}},$

то

$\frac{{CP \cdot DK}}{{BP}} = \frac{{BP \cdot DK}}{{CP}}\_\_\_\_\_\left| {:DK} \right.$

$\frac{{CP}}{{BP}} = \frac{{BP}}{{CP}}$

По основному свойству пропорции,

$CP^2 = BP^2 ,$

а значит, CP=BP, то есть P — середина BC.

Аналогично,

$CP = \frac{{BP \cdot AK}}{{DK}},CP = \frac{{BP \cdot DK}}{{AK}},$

$\frac{{BP \cdot AK}}{{DK}} = \frac{{BP \cdot DK}}{{AK}}\_\_\_\_\_\left| {:BP} \right.$

$\frac{{AK}}{{DK}} = \frac{{DK}}{{AK}},$

$AK^2 = DK^2 ,$

AK=DK, K — середина AD.

Что и требовалось доказать.

Альтернативный вариант.

Докажем, что медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.
Докажем, что точка пересечения диагоналей трапеции и середина её меньшего основания лежат на прямой, проходящей через точку пересечения продолжения боковых сторон трапеции и середину большего основания

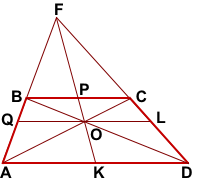trapeciya-zamechatelnoe-svojstvo В нашем случае докажем, что точки O и P лежат на прямой FK.

FK — медиана треугольника AFD.

Проведём через точку O пересечения диагоналей трапеции отрезок QL с концами на боковых сторонах трапеции.

BC||AD (как основания трапеции), QL||AD (по построению).

О — середина QL.

Так как медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника, то точки P и O лежат прямой FK.

И ещё.

Поскольку медиана FK, проведённая к AD, делит пополам любой отрезок, параллельный AD, с концами на сторонах AF и DF, то среднюю линию трапеции она также делит пополам. Таким образом, замечательное свойство трапеции можно дополнить:

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции, середины оснований трапеции и середина средней линии трапеции лежат на одной прямой.

Замечательное свойство трапеции

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики