Медиана делит пополам любой отрезок, параллельный стороне

Утверждение

Медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.

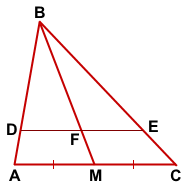Дано: ΔABC,

BM — медиана,

D∈AB, E∈BC, DE||AC,

DE∩BM=F

Доказать: DF=FE

Доказательство:

Рассмотрим треугольники ABM и DBF.

У них угол B — общий, ∠BAM=∠BDF (как соответственные при AC||DE и секущей AB).

Следовательно, треугольники ABM и DBF подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Аналогично, треугольники CBM и EBF подобны и

Правые части получившихся равенств равны, приравниваем левые части:

Так как BM — медиана, то AM=MC, то есть

Отсюда следует, что DF=FE.

Что и требовалось доказать.