Биссектриса треугольника делится в отношении |

Выясним, в каком отношении точка пересечения биссектрис треугольника делит каждую биссектрису.

Утверждение

Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.

bissektrisy-treugolnika-delyatsya-v-otnoshenii Дано:

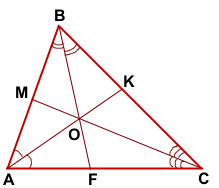
ΔABC,

AK, BF, CM — биссектрисы ΔABC,

AK∩BF=O

Доказать:

$\frac{{BO}}{{OF}} = \frac{{AB + BC}}{{AC}},$

$\frac{{AO}}{{OK}} = \frac{{AB + AC}}{{BC}},$

$\frac{{CO}}{{OM}} = \frac{{BC + AC}}{{AB}}.$

Доказательство:

Из треугольника ABF по свойству биссектрисы треугольника

$\frac{{AB}}{{AF}} = \frac{{BO}}{{OF}} \Rightarrow AB = \frac{{BO}}{{OF}} \cdot AF.$

Из треугольника CBF по свойству биссектрисы треугольника

$\frac{{CB}}{{CF}} = \frac{{BO}}{{OF}} \Rightarrow CB = \frac{{BO}}{{OF}} \cdot CF.$

Отсюда,

$AB + CB = \frac{{BO}}{{OF}} \cdot AF + \frac{{BO}}{{OF}} \cdot CF$

$AB + CB = \frac{{BO}}{{OF}}(AF + CF)$

$AB + CB = \frac{{BO}}{{OF}} \cdot AC$

Разделив обе части равенства на AC, получим

$\frac{{AB + CB}}{{AC}} = \frac{{BO}}{{OF}}.$

Два другие соотношения доказываются аналогично.

Что и требовалось доказать.

Так как согласно неравенству треугольника длина любой стороны треугольника меньше суммы двух других его сторон, то каждое из этих отношений больше единицы.

Задача

Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 22.

Дано: ΔABC,

AK, BF, CM — биссектрисы ΔABC,

AK∩BF=O, BO:OF=17:10, AC=22

Найти: P_ΔABC.

Решение:

По доказанному,

$\frac{{AB + CB}}{{AC}} = \frac{{BO}}{{OF}}$

(на экзамене в открытой части необходимо привести доказательство).

Следовательно, AB+BC=1,7AC.

P_ΔABC=AB+BC+AC=1,7AC+AC=2,7AC=2,7·22=59,4.

Ответ: 59,4.

Биссектриса треугольника делится в отношении

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики