Окружности касаются внешним образом

Задача

Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Соединим центры окружностей — точки O₁ и O₂ — с точками A и C соответственно.

O₁A⊥AC, O₂C⊥AC (как радиус, проведённый в точку касания).

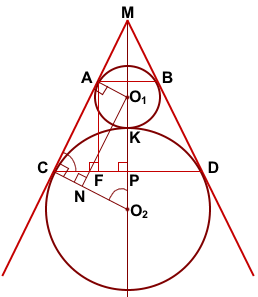Обозначим O₁A=r, O₂C=R.

Проведём перпендикуляр AF к прямой CD и перпендикуляр O₁N к прямой CO₂.

AF — искомое расстояние между прямыми AB и CD.

Четырёхугольник AO₁NC — прямоугольник (так как у него три угла прямые).

Следовательно, AC=O₁N, CN=O₁A=r.

Рассмотрим прямоугольный треугольник O₁O₂N.

NO₂=CO₂-CN=R-r.

По теореме Пифагора

   

O₁O₂= O₁K+KO₂=r+R,

   

   

Продлим касательные AC и BD до пересечения в точке M. Проведём луч MO₂.

Пусть MO₂∩CD=P.

Окружности с центрами в точках O₁ и O₂ вписаны в угол CMD, значит MP — биссектриса угла CMD.

MC=MD (как отрезки касательных, проведённых из одной точки). Значит треугольник CMD — равнобедренный с основанием CD. Следовательно, биссектриса MP является также его высотой.

В прямоугольном треугольнике CMP ∠MCP=90°-∠CMP.

В прямоугольном треугольнике CMO₂ ∠CO₂M=90°-∠CMP.

Отсюда ∠MCP=∠CO₂M. Следовательно, прямоугольные треугольники AFC и O₁NO₂ подобны (по острому углу).

Значит

   

   

   

Ответ: 112.