В трапеции ABCD биссектриса угла |

В равнобедренной трапеции ABCD биссектриса угла A пересекается

Задача

В равнобедренной трапеции ABCD с большим основанием AD биссектриса угла A пересекается с биссектрисой угла C в точке F, а также пересекает сторону CD в точке K. Известно, что прямые AB и CF параллельны. Найти CF, если FK=4√3.

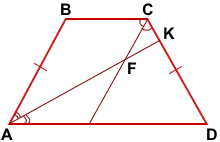v-trapecii-abcd-bissektrisa-ugla Дано: ABCD — трапеция, AD||BC, AB=CD,

AF — биссектриса ∠BAD, CF — биссектриса∠BCD,

CF||AB, AF∩CD=K, FK=4√3

Найти: CF

Решение:

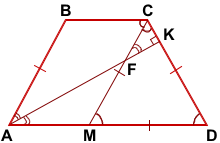v-ravnobedrennoj-trapecii-abcd-s-bolshim-osnovaniem-ad Пусть CF пересекает AD в точке M.

Так как биссектриса угла трапеции отсекает от неё равнобедренный треугольник, то ΔCDM — равнобедренный с основанием CM, то есть CD=MD.

CM||AB (по условию), AM||BC (как основания трапеции). Значит, четырёхугольник ABCM — параллелограмм и CM=AB (по свойству параллелограмма).

Поскольку CD=AB (по условию), то CM=CD=MD. Следовательно, треугольник CDM — равносторонний, все его углы равны по 60° и ∠MCD=60°.

∠BAD+∠BCD=180° (по свойству противолежащих углов равнобедренной трапеции).

Так как AF и CF — биссектрисы углов∠BAD и ∠BCD, то

$\angle BAK + \angle DAM = \frac{1}{2}\angle BAD + \frac{1}{2}\angle BCD =$

$= \frac{1}{2}(\angle BAD + \angle BCD) = \frac{1}{2} \cdot 180^o = 90^o .$

∠CFK=∠BAK (как соответственные при CM||AB и секущей AK).

Следовательно ∠CFK+∠DAM=90°.

По теореме о сумме углов треугольника в треугольнике CFK ∠CKF=90°.

По определению синуса

$\sin \angle FCK = \frac{{FK}}{{CF}},$

$CF = \frac{{FK}}{{\sin \angle FCK}} = \frac{{4\sqrt 3 }}{{\sin 60^o }} = \frac{{4\sqrt 3 }}{{\frac{{\sqrt 3 }}{2}}} = 8.$

Ответ: 8.

Добавить комментарий Отменить ответ