Задача
На стороне ромба построен равносторонний треугольник. Отрезок, соединяющий точку пересечения диагоналей ромба с серединой стороны треугольника, составляет с ней угол 70 градусов. Найти острый угол ромба.
Решение:
I способ
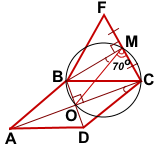 Пусть ABCD — ромб, треугольник BCF — равносторонний, M — середина FC, O — точка пересечения диагоналей ромба. По условию, ∠OMC=70°.
Пусть ABCD — ромб, треугольник BCF — равносторонний, M — середина FC, O — точка пересечения диагоналей ромба. По условию, ∠OMC=70°.
В треугольнике BMF проведём медиану BM. По свойству равностороннего треугольника BM является также его высотой, то есть BM ⊥ FC.
∠BMO=∠BMC-∠OMC=90-70=20°
Так как диагонали ромба перпендикулярны, то ∠BOC=90°.
В четырёхугольнике BMCO ∠BOC=90° и ∠BMC=90°.
Отсюда ∠BOC+∠BMC=180°. Следовательно, около BMCO можно описать окружность.
Поэтому ∠BCO=∠BMO=20° (как вписанные углы, опирающиеся на одну дугу OB).
Так как диагонали ромба являются биссектрисами его углов, ∠BCD=2∠BCO=40°.
Если точка M — середина BC, то FM⊥BC и ∠OMC=∠BOF=90° (как вертикальные). Это случай не соответствует условию.
Ответ: 40°.
II способ
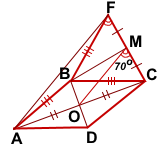 Точка M — середина отрезка FC по условию. Точка O — середина AC по свойству ромба. Следовательно, OM — средняя линия треугольника ACF.
Точка M — середина отрезка FC по условию. Точка O — середина AC по свойству ромба. Следовательно, OM — средняя линия треугольника ACF.
По свойству средней линии треугольника MO || AF.
∠AFC=∠OMC=70° (как соответственные при MO || AF и секущей FC).
∠BFC=∠FCB=60° (как углы равностороннего треугольника).
∠AFB=∠AFC-∠BFC=70-60=10°.
∠BAF=∠AFB=10° (как углы при основании равнобедренного треугольника ABF).
По свойствам ромба ∠BAC=∠BCA=x°.
Из треугольника AFC по теореме о сумме углов треугольника
∠AFC+∠FCA+∠FAC=180°,
70+60+x+x+10=180,
2x=40,
x=20.
Таким образом, ∠BCA=20°, ∠BCD=40°.

Вижу, мои комменты пригодились для второго способа решения?
Хотя и не получила ответного комментария!
«Наталия, углы BOC и BMC не накрест лежащие и не внутренние односторонние, поэтому BM не параллельна OC. Но вариант решения без окружности возможен, добавила второй способ» — комментарий был добавлен к посту, в котором Вы задавали вопрос (в свойстве медиан).