Четырехугольник, вписанный в окружность |

Рассмотрим, что такое четырехугольник, вписанный в окружность и около какого четырехугольника можно описать окружность.

Определение.

Четырехугольник называется вписанным в окружность, если все вершины четырехугольника лежат на окружности.

opredelenie chetyirehugolnika vpisannogo v okruzhnost

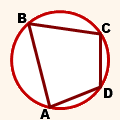
Четырехугольник ABCD — вписанный в окружность.

Все его вершины — точки A, B, C, D — лежат на окружности.

Теорема

1) Четырехугольник можно вписать в окружность, если сумма его противолежащих углов равна 180º.

2) Если сумма противолежащих углов четырехугольника равна 180º, то этот четырехугольник можно вписать в окружность.

Chetyirehugolnik vpisannyiy v okruzhnost

$\left. \begin{array}{l} \angle A + \angle C = {180^o}\\ \angle B + \angle D = {180^o} \end{array} \right\} \Leftrightarrow ABCD -$

вписанный в окружность.

Следствия.

1) Из всех параллелограммов вписать в окружность можно только прямоугольник (в том числе, в квадрат).

pryamougolnik vpisannyiy v okruzhnost Центр описанной около прямоугольника окружности — точка пересечения его диагоналей.

Радиус описанной около прямоугольника окружности равен половине его диагонали.

$R = \frac{1}{2}BD$

Через стороны прямоугольника радиус описанной окружности равен

$R = \frac{1}{2}\sqrt {A{B^2} + A{D^2}}$

Если стороны прямоугольника обозначить как a и b, то

$R = \frac{1}{2}\sqrt {{a^2} + {b^2}}$

2) Из всех трапеций вписать в окружность можно только равнобедренную трапецию.

trapetsiya vpisannaya v okruzhnost Радиус описанной около трапеции окружности можно найти как радиус окружности, описанной около одного из треугольников — вершин трапеции:

ABC, ABD, ACD или BCD.

Четырехугольник, вписанный в окружность