Радиус описанной около треугольника окружности можно найти по одной из двух общих формул.
Кроме того, для правильного и прямоугольного треугольников существуют дополнительные формулы.
Радиус описанной около произвольного треугольника окружности
Формула I (следствие из теоремы синусов)
![]()
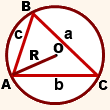
То есть радиус описанной окружности равен отношению длины стороны треугольника к удвоенному синусу противолежащего этой стороне угла.
В общем виде эту формулу записывают так:
![]()
Формула II.
![]()
в общем виде —
![]()
То есть чтобы найти радиус описанной около треугольника окружности, надо произведения длин сторон треугольника разделить на четыре площади треугольника.
Если площадь треугольника находить по формуле Герона
![]()
где p — полупериметр,
![]()
то получим формулу радиуса описанной около треугольника окружности через длины сторон:
![]()
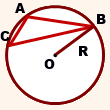
Обе эти формулы можно применить к треугольнику любого вида. Следует только учесть положение центра.
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника, напротив тупого угла.
Радиус окружности, описанной около прямоугольного треугольника
 Формула:
Формула:
![]()
То есть в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.
Обычно гипотенузу обозначают через c (AB=c) и формулу записывают так:
![]()
Радиус окружности, описанной около правильного треугольника
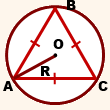
Формула:
![]()
Если без иррациональности в знаменателе, то
![]()
В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной окружности:
![]()

??????♥️