Площадь треугольника по сторонам |

Площадь треугольника по сторонам

Найти площадь треугольника по трем сторонам можно с помощью формулы Герона.

Формула Герона:

$S = \sqrt {p(p - a)(p - b)(p - c)} ,$

ploschad treugolnika po storonam

где p — полупериметр:

$p = \frac{{a + b + c}}{2}$

a, b, c — длины сторон треугольника.

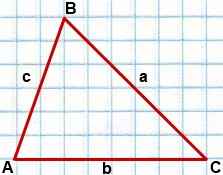
ploschad treugolnika po trem storonam

Дано:

∆ ABC,

AB=c, AC=b, BC=a,

$p = \frac{{a + b + c}}{2}$

Доказать:

${S_{\Delta ABC}} = \sqrt {p(p - a)(p - b)(p - c)} .$

Доказательство:

В любом треугольнике всегда есть два острых угла.

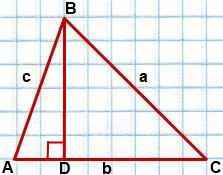
nayti ploschad treugolnika po storonam

Проведем в треугольнике ABC высоту BD при условии, что углы A и C- острые

(если треугольник ABC тупоугольный либо прямоугольный, то в качестве угла B выбираем тупой либо прямой угол).

По теореме Пифагора, из прямоугольного треугольника ABD

$B{D^2} = A{B^2} - A{D^2},$

из прямоугольного треугольника BCD —

$B{D^2} = B{C^2} - C{D^2}.$

Приравниваем правые части равенств:

$A{B^2} - A{D^2} = B{C^2} - C{D^2}.$

BC² перенесем в правую часть, AD² — в левую:

$A{B^2} - B{C^2} = A{D^2} - C{D^2}.$

$A{B^2} - B{C^2} = A{D^2} - C{D^2}.$

Правую часть разложим по формуле разности квадратов:

$A{B^2} - B{C^2} = (AD - CD)(AD + CD).$

Так как AD+CD=AC, то

$A{B^2} - B{C^2} = AC \cdot (AD - CD),$

${c^2} - {a^2} = b(AD - CD).$

Отсюда

$AD - CD = \frac{{{c^2} - {a^2}}}{b},AD + CD = b.$

Сложим эти два равенства почленно и приведем правую часть к общему знаменателю:

$AD - CD + AD + CD = \frac{{{c^2} - {a^2}}}{b} + {b^{\backslash b}}$

$2AD = \frac{{{c^2} - {a^2} + {b^2}}}{b},AD = \frac{{{c^2} - {a^2} + {b^2}}}{{2b}}.$

$B{D^2} = A{B^2} - A{D^2} = (AB - AD)(AB + AD) =$

$= ({c^{\backslash 2b}} - \frac{{{c^2} - {a^2} + {b^2}}}{{2b}})({c^{\backslash 2b}} + \frac{{{c^2} - {a^2} + {b^2}}}{{2b}}) =$

$= \frac{{2bc - ({c^2} - {a^2} + {b^2})}}{{2b}} \cdot \frac{{2bc + ({c^2} - {a^2} + {b^2})}}{{2b}} =$

$= \frac{{(2bc - {c^2} + {a^2} - {b^2})(2bc + {c^2} - {a^2} + {b^2})}}{{4{b^2}}} =$

$= \frac{{({a^2} - ({b^2} - 2bc + {c^2}))(({b^2} + 2bc + {c^2}) - {a^2})}}{{4{b^2}}} =$

$= \frac{{({a^2} - {{(b - c)}^2})({{(b + c)}^2} - {a^2})}}{{4{b^2}}} =$

$= \frac{{(a - (b - c))(a + b - c)(b + c - a)(b + c + a)}}{{4{b^2}}} =$

$= \frac{{(a - b + c)(a + b - c)(b + c - a)(b + c + a)}}{{4{b^2}}}$

Поскольку

$a + b + c = 2p,$

$a - b + c = a + b + c - 2b = 2p - 2b = 2(p - b),$

$a + b - c = a + b + c - 2c = 2p - 2c = 2(p - c),$

$b + c - a = a + b + c - 2a = 2p - 2a = 2(p - a),$

то

$B{D^2} = \frac{{2(p - b) \cdot 2(p - c) \cdot 2(p - a) \cdot 2p}}{{4{b^2}}} =$

$= \frac{{4p(p - b)(p - c)(p - a)}}{{{b^2}}}.$

Отсюда,

$BD = \sqrt {\frac{{4p(p - b)(p - c)(p - a)}}{{{b^2}}}} =$

$= \frac{{2\sqrt {p(p - b)(p - c)(p - a)} }}{b}.$

По формуле

$S = \frac{1}{2}a{h_a},$

площадь треугольника ABC равна

${S_{\Delta ABC}} = \frac{1}{2}AC \cdot BD.$

Таким образом,

${S_{\Delta ABC}} = \frac{1}{2} \cdot b \cdot \frac{{2\sqrt {p(p - b)(p - c)(p - a)} }}{b} =$

$= \sqrt {p(p - b)(p - c)(p - a)} .$

Что и требовалось доказать.

Добавить комментарий Отменить ответ