Площадь треугольника по двум сторонам

Выясним, как найти площадь треугольника по двум сторонам.

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Формула площади треугольника по двум сторонам:

formula ploschadi treugolnika po dvum storonam

$S = \frac{1}{2}ab\sin \alpha$

ploschad treugolnika po dvum storonam

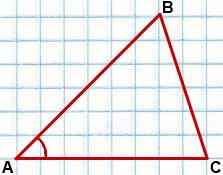
Дано:

∆ ABC.

Доказать:

${S_{\Delta ABC}} = \frac{1}{2}AB \cdot AC \cdot \sin \angle A$

Доказательство:

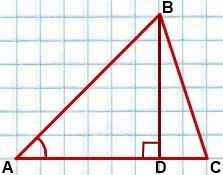
ploschad treugolnika po dvum storonam i sinusu ugla

Проведем в треугольнике ABC высоту BD.

равна половине произведения его стороны на высоту, проведенную к этой стороне:

${S_{\Delta ABC}} = \frac{1}{2}AC \cdot BD.$

Рассмотрим треугольник ABD — прямоугольный (так как BD — высота по построению).

По определению синуса острого угла в прямоугольном треугольнике,

$\sin \angle A = \frac{{BD}}{{AB}}.$

Отсюда

$BD = AB \cdot \sin \angle A.$

Таким образом,

${S_{\Delta ABC}} = \frac{1}{2}AC \cdot BD = \frac{1}{2}AC \cdot AB \cdot \sin \angle A.$

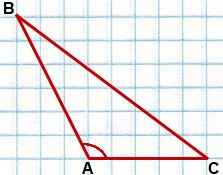
nayti ploschad treugolnika po dvum storonam i sinusu ugla

Если в треугольнике ABC

угол A тупой,

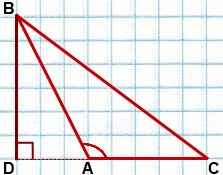
ploschad treugolnika cherez sinus

то в треугольнике ABD

$\angle BAD = {180^o} - \angle BAC$

$\sin ({180^o} - \alpha ) = \sin \alpha$

имеем:

$\sin \angle BAD = \sin ({180^o} - \angle BAC) =$

$= \sin \angle BAC = \sin \angle A.$

То есть, и в случае тупого угла A выполняется равенство

$BD = AB \cdot \sin \angle A,$

а значит, верна формула

${S_{\Delta ABC}} = \frac{1}{2}AB \cdot AC \cdot \sin \angle A.$

Что и требовалось доказать.