Какие углы вертикальные? Каким свойством обладают вертикальные углы?
Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.
Определение.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
При пересечении двух прямых образуется две пары вертикальных углов:

∠1 и ∠2 — вертикальные углы
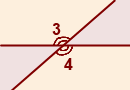
∠3 и ∠4 — вертикальные углы
Свойство вертикальных углов.
Вертикальные углы равны.

∠AOC =∠BOD

∠AOD =∠BOC
Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.
Задачи.
1) Сумма вертикальных углов равна 140º. Найти эти углы.
Решение:
Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.
Ответ: 70º, 70º.
2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.
Решение:
При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.
Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.
А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.
Ответ: 50º, 50º.
Вертикальные углы во многих задачах — важный элемент при доказательстве равенства треугольников и подобия треугольников.
