Выясним, в каком отношении точка пересечения биссектрис треугольника делит каждую биссектрису.
Утверждение
Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
Дано:
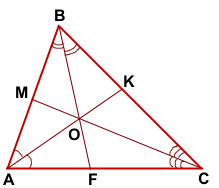
ΔABC,
AK, BF, CM — биссектрисы ΔABC,
AK∩BF=O
Доказать:
![\[ \frac{{BO}}{{OF}} = \frac{{AB + BC}}{{AC}}, \]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-c76cab653cfdf47394ab383a3aa8f2e6_l3.png "Rendered by QuickLaTeX.com")
Задача
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Решение:
Задача
В равнобедренной трапеции ABCD с большим основанием AD биссектриса угла A пересекается с биссектрисой угла C в точке F, а также пересекает сторону CD в точке K. Известно, что прямые AB и CF параллельны. Найти CF, если FK=4√3.
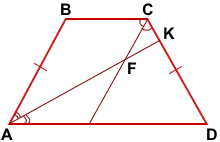Дано: ABCD — трапеция, AD||BC, AB=CD,
AF — биссектриса ∠BAD, CF — биссектриса∠BCD,
CF||AB, AF∩CD=K, FK=4√3
Найти: CF
Задача
На стороне ромба построен равносторонний треугольник. Отрезок, соединяющий точку пересечения диагоналей ромба с серединой стороны треугольника, составляет с ней угол 70 градусов. Найти острый угол ромба.
Решение:
Теорема (Птолемея)
Произведение диагоналей вписанного четырёхугольника равно сумме произведений двух пар его противолежащих сторон.
Дано:
4-угольник ABCD вписан в окр. (O; R)
Доказать:
AC·BD=AB·CD+AD·BC
Доказательство:
Утверждение
Если диагонали вписанного четырехугольника перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности.
Дано:
окружность (O;d),
ABCD — вписанный четырёхугольник,
AC⊥BD
Доказать: AD² +BC² = d²
Доказательство:
Утверждение 1
Если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов его противолежащих сторон равны.
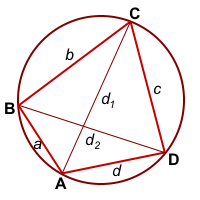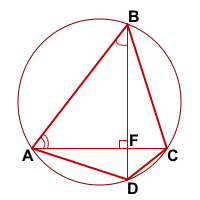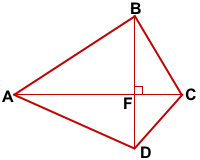Дано: ABCD — выпуклый четырёхугольник,
AC⊥BD
Доказать:
AB²+CD²=AD²+BC²
Доказательство: