диагонали четырехугольника перпендикулярны |

Если диагонали четырехугольника перпендикулярны

Утверждение 1

Если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов его противолежащих сторон равны.

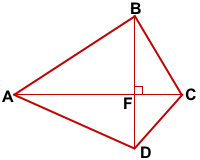diagonali-chetyrekhugolnika-perpendikulyarny Дано: ABCD — выпуклый четырёхугольник,

AC⊥BD

Доказать:

AB²+CD²=AD²+BC²

Доказательство:

Из прямоугольных треугольников AFB, CFD, AFD и BFC по теореме Пифагора

$AB^2 = AF^2 + BF^2 ,$

$CD^2 = CF^2 + DF^2 ,$

$AD^2 = AF^2 + DF^2 ,$

$BC^2 = BF^2 + CF^2 .$

Сложив почленно 1-е и 2-е равенства, получим

$+ \frac{\begin{array}{l} AB^2 = AF^2 + BF^2 \\ CD^2 = CF^2 + DF^2 \\ \end{array}}{{AB^2 + CD^2 = AF^2 + BF^2 + CF^2 + DF^2 }},$

$AB^2 + CD^2 = (AF^2 + DF^2 ) + (BF^2 + CF^2 ) = AD^2 + BC^2 .$

Что и требовалось доказать.

Утверждение 2

Если суммы квадратов противолежащих сторон выпуклого четырехугольника равны, то его диагонали взаимно перпендикулярны.

(Чертеж — тот же).

Дано: ABCD — выпуклый четырёхугольник,

AB²+CD²=AD²+BC²

Доказать: AC⊥BD

Доказательство:

Пусть ∠AFB=α.

∠AFB+∠BFC=180° (как смежные).

∠CFD=∠AFB=α, ∠AFD=∠BFC=180°-α (как вертикальные).

cos∠BFC=cos∠AFD=cos (180°-α)= -cosα.

Из треугольников AFB, CFD, AFD и BFC по теореме косинусов

$AB^2 = AF^2 + BF^2 - 2AB \cdot BF \cdot \cos \alpha ,$

$CD^2 = CF^2 + DF^2 - 2CF \cdot DF \cdot \cos \alpha ,$

$AD^2 = AF^2 + DF^2 + 2AF \cdot DF \cdot \cos \alpha ,$

$BC^2 = BF^2 + CF^2 + 2BF \cdot CF \cdot \cos \alpha .$

Так как AB²+CD²=AD²+BC² (по условию), то

$AF^2 + BF^2 - 2AB \cdot BF \cdot \cos \alpha +$

$+ CF^2 + DF^2 - 2CF \cdot DF \cdot \cos \alpha =$

$= AF^2 + DF^2 + 2AF \cdot DF \cdot \cos \alpha +$

$+ BF^2 + CF^2 + 2BF \cdot CF \cdot \cos \alpha ,$

откуда

$- 2AB \cdot BF \cdot \cos \alpha - 2CF \cdot DF \cdot \cos \alpha =$

$= 2AF \cdot DF \cdot \cos \alpha + 2BF \cdot CF \cdot \cos \alpha ,$

$AB \cdot BF \cdot \cos \alpha + CF \cdot DF \cdot \cos \alpha +$

$+ AF \cdot DF \cdot \cos \alpha + BF \cdot CF \cdot \cos \alpha = 0,$

$\cos \alpha (AB \cdot BF + CF \cdot DF + AF \cdot DF + BF \cdot CF) = 0.$

Произведение равно нулю, если хотя бы один из множителей равняется нулю.

$AB \cdot BF + CF \cdot DF + AF \cdot DF + BF \cdot CF \ne 0$

(как сумма положительных слагаемых), следовательно cosα=0.

Значит α=90°, то есть AC⊥BD.

Что и требовалось доказать.

Добавить комментарий Отменить ответ