Если диагонали вписанного четырехугольника перпендикулярны

Если диагонали вписанного четырехугольника перпендикулярны

Jun.30,2019

Утверждение

Если диагонали вписанного четырехугольника перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности.

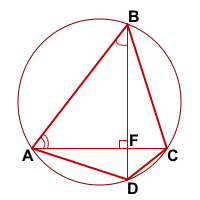diagonali-vpisannogo-chetyrekhugolnika Дано:

окружность (O;d),

ABCD — вписанный четырёхугольник,

AC⊥BD

Доказать: AD² +BC² = d²

Доказательство:

I способ

Радиус и диаметр описанной около треугольника окружности можно найти по формуле

$2R = d = \frac{a}{{\sin \alpha }},$

где α — угол, противолежащий стороне a.

Для вписанного треугольника ABD

$d = \frac{{AD}}{{\sin \angle ABD}},$

откуда

$AD = d \cdot \sin \angle ABD.$

Для треугольника ABC —

$d = \frac{{BC}}{{\sin \angle BAC}},$

$BC = d \cdot \sin \angle BAC.$

Обозначим точку пересечения диагоналей четырёхугольника ABCD как F.

В прямоугольном треугольнике ABF по определению синуса и косинуса

$\sin \angle BAC = \frac{{BF}}{{AB}} = \cos \angle ABD.$

$AD^2 + BC^2 = (d \cdot \sin \angle ABD)^2 + (d \cdot \sin \angle BAC)^2 =$

$= d^2 (\sin ^2 \angle ABD + \sin ^2 \angle BAC) =$

$= d^2 (\sin ^2 \angle ABD + \cos ^2 \angle ABD) = d^2 \cdot 1 = d^2 .$

Что и требовалось доказать.

II способ

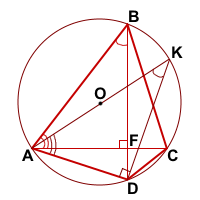diagonali-vpisannogo-chetyrekhugolnika-perpendikulyarny Проведём диаметр AK, AK=d.

Рассмотрим треугольник ADK.

∠ADK=90° (как вписанный угол, опирающийся на диаметр).

По теореме Пифагора

$AD^2 + KD^2 = AK^2 ,$

то есть

$AD^2 + KD^2 = d^2 .$

Так как сумма острых углов прямоугольного треугольника равна 90°, то ∠KAD=90°-∠AKD.

∠AKD=∠ABD (как вписанные углы, опирающиеся на одну дугу AD).

В прямоугольном треугольнике ABF ∠BAF=90°-∠ABF=90°-∠ABD=90°-∠AKD=∠KAD.

Таким образом, ∪KD=2∠KAD, ∪BC=2∠BAC, ∠BAC=∠KAD. Поэтому ∪KD=∪BC.

Так как дуги равны, то они стягивают равные хорды, то есть KD=BC.

Отсюда

$AD^2 + BC^2 = d^2 .$

Следовательно, AB²+CD²=AD²+BC²=d² (=4R²).

Что и требовалось доказать.

Добавить комментарий Отменить ответ