Если две медианы треугольника равны

Утверждение

Если две медианы треугольника равны, то этот треугольник — равнобедренный.

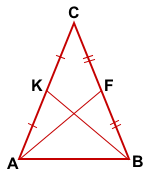Дано: ΔABC,

AF, BK — медианы,

AF=BK

Доказать: ΔABC — равнобедренный

Доказательство:

I способ

Так как AF и BK — медианы треугольника ABC, то точки F и K — середины отрезков BC  и AC соответственно.

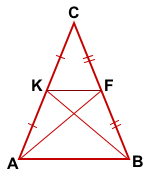Значит KF — средняя линия ΔABC.

По свойству средней линии треугольника, KF || AB.

Таким образом, AKFB — трапеция.

Поскольку AF=BK, то трапеция AKFB — равнобедренная, то есть AK=BF.

Половины отрезков равны, значит равны и сами отрезки: AC=BC.

Следовательно, треугольник ABC — равнобедренный с основанием AB.

Что и требовалось доказать.

II способ

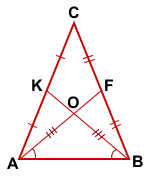Пусть AF∩BK=O.

Так как медианы треугольника точкой пересечения делятся в отношении 2 к 1, считая от вершины, то

   

   

Так как AF=BK (по условию), то AO=BO.

Следовательно, треугольник AOB — равнобедренный с основанием AB.

Отсюда ∠OAB=∠OBA (как углы при основании).

Рассмотрим треугольники ABF и BAK.

1)AF=BK (по условию),

2) сторона AB — общая,

3) ∠OAB=∠OBA (по доказанному).

Значит треугольники ABF и BAK равны ( по 1 признаку).

Из равенства треугольников следует равенство соответствующих углов:∠ABF=∠BAK.

Отсюда треугольник ABC — равнобедренный с основанием AB (по признаку).

Что и требовалось доказать.