Что такое равнобедренный треугольник?
Рассмотрим определение равнобедренного треугольника и выясним, как называются его стороны и углы.
Определение
Равнобедренный треугольник — это треугольник, в котором две стороны равны.
Эти равные стороны называются боковыми, а третья сторона называется основанием равнобедренного треугольника.
Вершина равнобедренного треугольника — это та вершина, которая лежит напротив основания.
Угол, лежащий напротив основания — угол при вершине равнобедренного треугольника.
Два другие угла — углы при основании равнобедренного треугольника.
Виды равнобедренных треугольников:
1) остроугольный — все углы острые;
2) прямоугольный — угол при вершине — прямой (при основании — острые);
3) тупоугольный — угол при вершине — тупой (при основании — острые);
4) равносторонний — все стороны равны и все углы равны.
Рисунок равнобедренного треугольника удобно делать по клеточкам.
Названия сторон равнобедренного треугольника — основание, боковая сторона, — как бы предполагают, что основание равнобедренного треугольника лежит внизу, а боковые стороны — по бокам.
Чаще всего равнобедренный треугольник именно так и изображают.
Но не всегда на рисунке равнобедренный треугольник имеет такой вид.
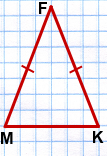Например, в треугольнике MKF
основание — MK,
боковые стороны — MF и KF.
F — вершина равнобедренного треугольника MKF.
∠F — угол при вершине,
∠M и ∠K — углы при основании.
В треугольнике ABC AC=BC.
Равные стороны являются боковыми.
Значит, боковые стороны треугольника ABC — это AC и BC,
а основание — AB.
C — вершина. ∠C — угол при вершине, а ∠A и ∠B — углы при основании равнобедренного треугольника ABC.
Знание свойств равнобедренного треугольника и умение их применять — обязательное условие успешного решения значительного количества геометрических задач.