Боковые стороны AB и CD трапеции

Задача

Боковые стороны AB и CD трапеции ABCD равны соответственно16 и 34, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB.Найти площадь трапеции.

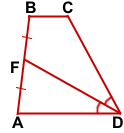Дано: ABCD — трапеция, AD || BC, BC=2,

AB=16, CD=34, DF — биссектриса ∠ADC, F — середина AB

Найти: S_ABCD

Решение:

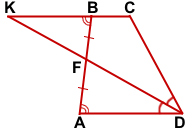Продолжим прямые DF и BC до пересечения в точке K.

Так как биссектриса трапеции отсекает от неё равнобедренный треугольник,  то CK=CD=34.

BK=CK-BC=34-2=32.

В треугольниках AFD и BFK:

1)AF=BF (по условию);

2)∠AFD=∠BFK (как вертикальные);

3) ∠DAF=∠KBF (как внутренние накрест лежащие при AD || BC и секущей AB).

Значит, треугольники AFD и BFK равны (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: AD=BK=32.

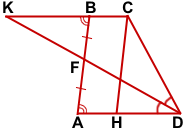Проведём через точку C прямую CH, параллельную прямой AB.

Четырёхугольник ABCH — параллелограмм. Следовательно, его противоположные стороны равны: AH=BC=2, CH=AB=16.

Отсюда HD=AD-AH=32-2=30.

Рассмотрим треугольник CHD.

34²=1156, 30²=900, 16²=256, то есть

   

По теореме, обратной теореме Пифагора, треугольник CHD — прямоугольный. Таким образом, CH⊥HD, CH — высота трапеции ABCD и

   

Ответ: 272.