Как найти площадь равнобедренного треугольника? Это можно сделать с помощью любой из формул для площади треугольника. Свойства равнобедренного треугольника эти формулы могут несколько видоизменить.
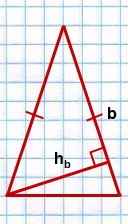
I. Площадь треугольника равна половине произведения стороны на проведенную к этой стороне высоту.

![]()
![]()
В равнобедренном треугольнике высота, проведенная к основанию, совпадает с медианой. Поэтому FC=1/2 BC, то есть
![]()
Этот факт стоит использовать, например, если нужно найти площадь равнобедренного треугольника, и известны его боковая сторона и высота, проведенная к основанию. В этом случае из прямоугольного треугольника треугольника AFC по теореме Пифагора найдем FC,
![]()
а затем сразу же — площадь
![]()
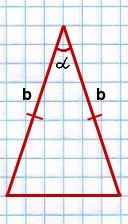
II. Площадь треугольника равна половине произведения двух сторон на синус угла между ними.

![]()
![]()
III. Площадь треугольника по трем сторонам ищут по формуле Герона. Поскольку в равнобедренном треугольнике две стороны равны, формула Герона для равнобедренного треугольника приобретает вид:
![]()
![]()
![]()
Полупериметр
![]()
поэтому
![]()
![]()
![]()
Специально запоминать эту формулу не нужно — практически, это формула из пункта I.
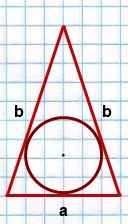
IV. Площадь треугольника через радиус вписанной окружности равна произведению радиуса на полупериметр.
Для равнобедренного треугольника
![]()
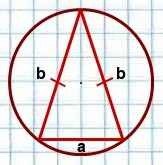
V. Площадь треугольника через радиус описанной окружности для равнобедренного треугольника приобретает вид:
![]()
