Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
 То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
![]()
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
 Если MN —
Если MN —
средняя линия
трапеции ABCD,
AD||BC, то
![]()
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
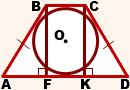 По свойству равнобедренной трапеции,
По свойству равнобедренной трапеции,
![]()
Если AD=a, BC=b,
![]()
![]()
Из прямоугольного треугольника ABF по теореме Пифагора
![]()
![]()
![]()
![]()
![]()
![]()
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
![]()
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

AK=AP=DP=DN,
BK=BF=CF=CN.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.
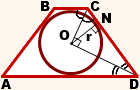 Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
![]()
Значит, треугольник COD — прямоугольный,
![]()
(как радиус, проведенный в точку касания).
Следовательно, ON — высота, проведённая к гипотенузе,
![]()
