Вписанная в трапецию окружность

Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?

1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.

1) В трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.

 

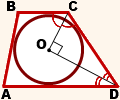
2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.

O — точка пересечения

биссектрис трапеции ABCD.

3. По свойству биссектрис трапеции, прилежащие к её боковой стороне,

   

   

и точка O лежит на средней линии трапеции.

4. Точки касания, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины:

AK=AP,

BK=BF,

CF=CN,

DN=DP (как отрезки касательных, проведённых из одной точки).

5.

   

   

   

   

(как радиусы, проведенные в точку касания).

6. Диаметр вписанной в трапецию окружности равен высоте трапеции, радиус — половине высоты: