Определение
Сумма векторов
![]()
и
![]()
— это вектор
![]()
с координатами c1=a1+b1, c2=a2+b2, то есть
![]()
или
![]()
Свойства сложения векторов:
Для любых векторов
![]()
верны свойства:
1) переместительное:
![]()
2) сочетательное:
![]()
3) свойство прибавления нулевого вектора:
![]()
4) сумма противоположных векторов равна нулевому вектору:
![]()
Доказательство:
Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:
![]()
![]()
Так как соответствующие координаты равны, то эти векторы равны.
Аналогично
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Теорема
(О сложении векторов)
Каковы бы ни были точки A, B, C, имеет место векторное равенство:
![]()
Доказательство:
Для точек A (x1;y1), B (x2;y2), C (x3;y3)
![]()
![]()
![]()
Тогда
![]()
![]()
Что и требовалось доказать.
Правило треугольника построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.
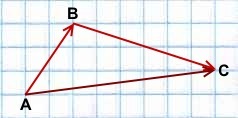 Например,
Например,
![]()
(то есть это правило следует из теоремы о сложении векторов).
Правило параллелограмма построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.
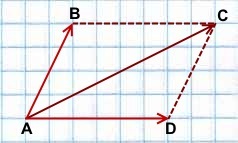 Например,
Например,
![]()
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.
При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.
Пример.
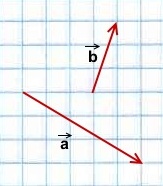 Построить сумму векторов
Построить сумму векторов
![]()
Решение:
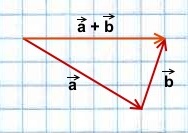
1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора
![]()
вектор
![]()
Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).
2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы
![]()
от общего начала.
Достроим на этих векторах параллелограмм.
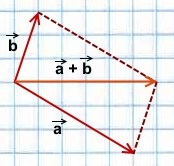 Сумма
Сумма
![]()
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.
Сложение коллинеарных векторов
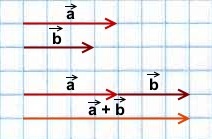
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.
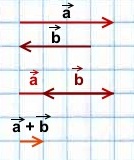
2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.
Фактически в обоих случаях мы используем правило треугольника сложения векторов:
от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.
Из неравенства треугольника следует ещё два свойства сложения векторов:
![]()
![]()
