Равные векторы |

В различных школьных учебниках определение равных векторов даётся по-разному.

В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.

Определение 1

Два вектора называются равными, если они совмещаются параллельным переносом.

(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).

ravnye-vektory Например, изображенные на рисунке

$\overrightarrow {AB}$

$\overrightarrow {CD}$

— равные векторы.

Равенство векторов обозначают так:

$\overrightarrow {AB} = \overrightarrow {CD}$

Теорема

(Свойства равных векторов)

1) Равные векторы сонаправлены и имеют равные длины.

2) Равные векторы имеют равные координаты.

3) От любой точки можно отложить вектор, равный данному, и притом только один.

Доказательство:

1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.

2) Пусть дан вектор

$\overrightarrow {AB}$

с началом в точке A(x₁; y₁) и концом в точке B(x₂; y₂).

По определению равных векторов, вектор

$\overrightarrow {A^/ B^/ }$

равный данному, получен из

$\overrightarrow {AB}$

параллельным переносом.

Если этот параллельный перенос задан формулами

$\left\{ \begin{array}{l} x^/ = x + m, \\ y^/ = y + n, \\ \end{array} \right.$

то A′(x₁+m; y₁+n), B′(x₂+m; y₂+n).

Найдём координаты каждого из векторов:

$\overrightarrow {AB} (x_2 - x_1 ;y_2 - y_1 ),$

$\overrightarrow {A^/ B^/ } ((x_2 + m) - (x_1 + m);(y_2 + n) - (y_1 + n)),$

$\overrightarrow {A^/ B^/ } (x_2 + m - x_1 - m;y_2 + n - y_1 - n),$

$\overrightarrow {A^/ B^/ } (x_2 - x_1 ;y_2 - y_1 ).$

То есть координаты равных векторов

$\overrightarrow {AB}$

$\overrightarrow {A^/ B^/ }$

равны.

Что и требовалось доказать.

Таким образом, координаты задают длину и направление вектора, но не фиксируют его.

3) Пусть даны вектор

$\overrightarrow {AB}$

и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор

$\overrightarrow {AC}$

При таком параллельном переносе вектор

$\overrightarrow {AB}$

переходит в вектор

$\overrightarrow {CD.}$

По определению равных векторов,

$\overrightarrow {CD} = \overrightarrow {AB} .$

Что и требовалось доказать.

На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).

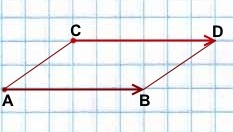postroit-vektor-ravnyj-dannomu Например,

вектор

$\overrightarrow {CD} ,$

отложенный от точки C, равен вектору

$\overrightarrow {AB}$

Теорема

(Признаки равенства векторов)

1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.

2) Если у векторов соответствующие координаты равны, то векторы равны.

Доказательство:

1) 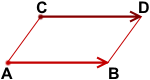priznaki-ravenstva-vektorov Пусть векторы

$\overrightarrow {AB}$

$\overrightarrow {CD}$

сонаправлены и имеют одинаковые длины.

Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор

$\overrightarrow {AB}$

переводит в вектор

$\overrightarrow {CD}$

По определению равных векторов,

$\overrightarrow {CD} = \overrightarrow {AB} .$

Что и требовалось доказать.

2) Пусть векторы

$\overrightarrow {AB}$

$\overrightarrow {A^/ B^/ }$

имеют равные координаты.
Если A(x₁; y₁), B(x₂; y₂), A′(x′₁; y′₁), B′(x′₂; y′₂), то по условию x₂-x₁=x′₂-x′₁,y₂-y₁=y′₂-y′₁.

Отсюда x′₂=x₂+x′₁-x₁, y′₂ =y₂+y′₁-y₁.

Параллельный перенос, заданный формулами

$\left\{ \begin{array}{l} x^/ = x - x_1 + x_1^/ , \\ y^/ = y - y_1 + y_1^/ , \\ \end{array} \right.$

переводит точку A в точку A′, точку B — в точку B′, то есть совмещает векторы

$\overrightarrow {AB}$

$\overrightarrow {A^/ B^/ }$

А это означает, что

$\overrightarrow {A^/ B^/ } = \overrightarrow {AB} .$

Что и требовалось доказать.

В учебнике Атанасяна Л. С. и др. дано другое определение равных векторов.

Определение 2

Два вектора называются равными, если они сонаправлены и имеют одинаковую длину.

Равные векторы

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики