Площадь прямоугольной трапеции |

Площадь прямоугольной трапеции

Площадь прямоугольной трапеции можно найти по любой из формул для площади произвольной трапеции. Некоторые из общих формул могут быть упрощены на основании свойств прямоугольной трапеции.

I. Площадь трапеции равна произведению полусуммы оснований на высоту.

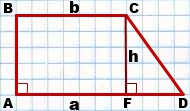ploshchad-pryamougolnoj-trapecii Площадь прямоугольной трапеции ABCD,

AD∥BC,

$AB \bot AD,CF \bot AD$

равна

${S_{ABCD}} = \frac{{AD + BC}}{2} \cdot CF$

Так как меньшая боковая сторона прямоугольной трапеции перпендикулярна основаниям, то она равна высоте трапеции, то есть

${S_{ABCD}} = \frac{{AD + BC}}{2} \cdot AB$

Если обозначить AD=a, BC=b, CF=AB=h, то формула площади прямоугольной трапеции через основания и высоту (меньшую боковую сторону):

$S = \frac{{a + b}}{2} \cdot h$

II. Площадь трапеции равна произведению средней линии на высоту.

ploshchad-pryamougolnoj-trapecii-cherez-srednyuyu-liniyu Если MN — средняя линия прямоугольной трапеции ABCD,

$AB \bot AD,$

то площадь

${S_{ABCD}} = MN \cdot AB$

Если обозначить среднюю линию MN=m, меньшую боковую сторону AB=h, получим формулу для нахождения площади прямоугольной трапеции через среднюю линию:

$S = m \cdot h$

III. Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.

ploshchad-pryamougolnoj-trapecii-cherez-diagonali Для прямоугольной

трапеции

ABCD,

AD∥BC,

${S_{ABCD}} = \frac{1}{2}AC \cdot BD \cdot \sin \angle COD$

Так как sin(180º-α)=sin α, то также

${S_{ABCD}} = \frac{1}{2}AC \cdot BD \cdot \sin \angle AOD$

Если AC=d1, BD=d2, ∠COD=φ, то

$S = \frac{1}{2}{d_1} \cdot {d_2} \cdot \sin \varphi$

ploshchad-pryamougolnoj-trapecii-cherez-perpendikulyarnye-diagonali В частности, если диагонали трапеции перпендикулярны, то

$S = \frac{1}{2}{d_1} \cdot {d_2}$

VI. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

ploshchad-pryamougolnoj-trapecii-cherez-radius

$S = p \cdot r$

Так как в трапецию можно вписать окружность, то

AD+BC=AB+CD=p. Следовательно,

${S_{ABCD}} = (AD + BC) \cdot r$

или

${S_{ABCD}} = (AB + CD) \cdot r$

Обозначив AD=a, BC=b, CD=c, AB=h=2r, получим формулы площади прямоугольной трапеции через радиус вписанной окружности:

$S = (a + b) \cdot r$

$S = (2r + c) \cdot r$

Если в трапецию вписана окружность, площадь трапеции также можно найти как удвоенное произведение радиуса и средней линии. Формула

$S = 2mr$

Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.

${S_{ABCD}} = AD \cdot BC$

или

$S = ab$

Добавить комментарий Отменить ответ