Условие параллельности прямых

I. Выясним, когда две прямые, заданные уравнениями y=k₁x+b₁ и y=k₂x+b₂, параллельны.

Число k₁ — угловой коэффициент прямой y=k₁x+b₁ — равно тангенсу угла, который данная прямая образует с положительным направлением оси абсцисс:

k₁ = tg α₁.

Аналогично, угловой коэффициент k₂ прямой y=k₂x+b₂ характеризует угол между этой прямой и положительным направлением оси Ox:

k₂ = tg α₂.

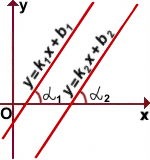uslovie-parallelnosti-pryamyh По признаку параллельности прямых y=k₁x+b₁ и y=k₂x+b₂ параллельны,если соответственные углы α₁ и α₂ равны.

Из равенства углов следует равенство тангенсов этих углов (180º<α<0°):

α₁= α₂⇒ tg α₁ = tg α₂.

А так как k₁ =tg α₁, k₂ = tg α₂, то получаем

условие параллельности прямых:

прямые, заданные уравнениями y=k₁x+b₁ и y=k₂x+b₂, параллельны, если их угловые коэффициенты равны:

k₁ = k₂ .

$a_1 x + b_1 y + c_1 = 0,$

$a_2 x + b_2 y + c_2 = 0$

угловые коэффициенты

$k_1 = - \frac{{a_1 }}{{b_1 }},k_2 = - \frac{{a_2 }}{{b_2 }}.$

Отсюда

$- \frac{{a_1 }}{{b_1 }} = - \frac{{a_2 }}{{b_2 }}$

и получаем условие параллельности для прямых a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0:

$\frac{{a_1 }}{{a_2 }} = \frac{{b_1 }}{{b_2 }}$