Уравнение прямой с угловым коэффициентом

Рассмотрим три случая положения прямой в координатной плоскости.

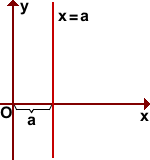1) Если прямая параллельна оси Oy.

В этом случае все её точки имеют одинаковые абсциссы. Например, если точка пересечения прямой с осью Ox имеет абсциссу a, то для всех точек прямой верно равенство

   

Это равенство является уравнением прямой, параллельной оси Oy.

2) Если прямая параллельна оси Ox.

Все точки прямой имеют одинаковые ординаты. Если точка пересечения прямой с осью Oy имеет ординату b, то для всех точек прямой верно равенство

   

это равенство является уравнением прямой, параллельной оси Ox.

 

3) Если прямая не параллельна ни одной из осей.

Пусть α — угол, который прямая образует с положительным направлением оси Ox, b — ордината точки пересечения прямой с осью Oy.

Выберем на прямой произвольную точку A(x;y). Проведём через точку A прямые, параллельные осям.

Рассмотрим образованный этими прямыми прямоугольный треугольник ABC.

AC=y-b, BC=x, ∠ABC=α (как соответственные при BC∥Ox и секущей AB).

По определению тангенса

   

Обозначим tgα=k. Число k называют угловым коэффициентом прямой  (эта величина играет очень важную роль). Тогда

   

откуда

   

Это уравнение называют уравнением прямой с угловым коэффициентом.

Если A — точка, лежащая не в I четверти, рассуждения усложняются, но в результате приходим к тому же уравнению: y=kx+b.

Если угол α — тупой, в прямоугольном треугольнике находят тангенс угла, смежного с α.

Уравнение y=b можно считать частным случаем уравнения y=kx+b, что согласуется с геометрическим смыслом k, поскольку для прямой, параллельной оси Oy, α=0°, а tg0°=0.

Для прямой, параллельной оси Oy, уравнение x=a не является частным случаем уравнения y=kx+b (что также согласуется с геометрическим смыслом k, так как в этом случае α=90°, а tg 90° не существует).

Таким образом, уравнение прямой с угловым коэффициентом задает все прямые, не параллельные оси Oy:

y=kx+b или y=b.

Прямые, параллельные оси Oy, задаются уравнением x=a другого вида.