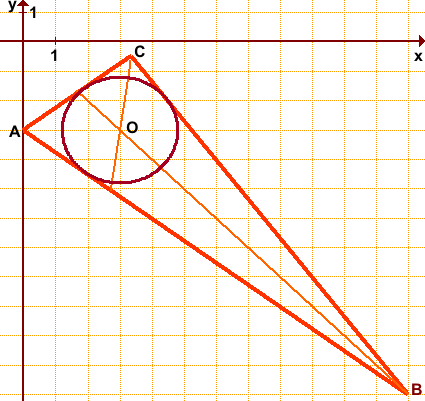Точка пересечения биссектрис |

Как найти точку пересечения биссектрис треугольника по координатам его вершин?

Как найти радиус вписанной в треугольник окружности по координатам его вершин?

Точка пересечения биссектрис треугольника является центром вписанной в этот треугольник окружности.

Эта точка равноудалена от сторон треугольника. Расстояние от точки пересечения биссектрис до сторон треугольника равно радиусу вписанной окружности.

Следовательно, все три задачи сводятся к нахождению точки пересечения биссектрис треугольника.

Для этого надо сначала составить уравнения биссектрис треугольника и найти точку их пересечения.

Пример.

Дан треугольник ABC с вершинами в точках A(0;-3), B(12;-12) и C(3,36;-0,48).

1) Найти точку пересечения биссектрис треугольника ABC.

2) Найти радиус вписанной в треугольник ABC окружности.

3) Составить уравнение вписанной в треугольник ABC окружности.

Решение:

1) Составим уравнения прямых, содержащих стороны треугольника.

Уравнение прямой, проходящей через две точки можно искать, например, в виде

$\frac{{y - y_1 }}{{y_2 - y_1 }} = \frac{{x - x_1 }}{{x_2 - x_1 }}$

Для прямой AB

$\frac{{y - ( - 3)}}{{ - 12 - ( - 3)}} = \frac{{x - 0}}{{12 - 0}},$

$12(y + 3) = - 9x,$

$3x + 4y + 12 = 0.$

Уравнение прямой AC:

$\frac{{y - ( - 3)}}{{ - 0,48 - ( - 3)}} = \frac{{x - 0}}{{3,36 - 0}},$

$3,36(y + 3) = 2,52x,$

$2,52x - 3,36y - 10,08 = 0,$

$3x - 4y - 12 = 0.$

Уравнение прямой BC:

$\frac{{y - ( - 12)}}{{ - 0,48 - ( - 12)}} = \frac{{x - 12}}{{3,36 - 12}},$

$- 8,64(y + 12) = 11,52(x - 12),$

$- 3(y + 12) = 4(x - 12),$

$4x + 3y - 12 = 0.$

Составим уравнение биссектрисы треугольника ABC, исходящей из угла B. Она образована прямыми AB и BC:

$\frac{{3x + 4y + 12}}{{\sqrt {3^2 + 4^2 } }} = \pm \frac{{4x + 3y - 12}}{{\sqrt {4^2 + 3^2 } }},$

откуда уравнения биссектрис угла B: x-y-24=0 или x+y=0. Чтобы понять, которое из двух уравнений является биссектрисой внутреннего угла треугольника, следует подставить в уравнения координаты точек A и C. Поскольку они лежат по разные стороны от биссектрисы внутреннего угла B, то подстановка их координат в уравнение биссектрисы даёт числа разных знаков.

A(0;-3) и C(3,36;-0,48) в x-y-24=0: 0-(-3)-24<0; 3,36-(-0,48)-24<0. Получили числа одного знака, значит это уравнение не является биссектрисой внутреннего угла треугольника.

A(0;-3) и C(3,36;-0,48) в x+y=0: 0+(-3)<0, 3,36+(-0,48)>0. Получили числа разных знаков, x+y=0 — биссектриса угла B треугольника ABC.

Составим уравнение биссектрисы угла C. Угол C образован прямыми AC и BC, откуда

$\frac{{3x - 4y - 12}}{{\sqrt {3^2 + ( - 4)^2 } }} = \frac{{4x + 3y - 12}}{{\sqrt {4^2 + 3^2 } }},$

уравнения биссектрис угла C: 7x-y-24=0 и x+7y=0.

A(0;-3), B(12;-12) в 7x-y-24=0: 7·0-(-3)-24<0, 7·12-(-12)-24>0. Получили числа разных знаков, значит 7x-y-24=0 — уравнение биссектрисы внутреннего угла C.

Поскольку все три биссектрисы треугольника пересекаются в одной точке, третью биссектрису находить не требуется.

Точку пересечения биссектрис углов B и C найдём из системы уравнений

$\left\{ \begin{array}{l} x + y = 0, \\ 7x - y - 24 = 0, \\ \end{array} \right.$

O(3;-3) — точка пересечения биссектрис треугольника ABC. Эта точка является центром вписанной в треугольник окружности.

2) Радиус вписанной в треугольник ABC окружности можно найти как расстояние от точки O до прямой AB, BC или AC. Найдем, например, расстояние от O до AB:

$r = \left| {OF} \right| = \frac{{\left| {3 \cdot 3 + 4 \cdot ( - 3) + 12} \right|}}{{\sqrt {4^2 + 3^2 } }} = \frac{9}{5}.$