Высота треугольника

В отличие от медианы или биссектрисы, высота треугольника может быть расположена как внутри треугольника, так и вне его.

Определение.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.

 

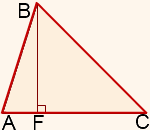
На рисунке BF — высота, проведенная из вершины B к стороне AC.

 

 

Все три высоты треугольника, либо прямые, содержащие высоты треугольника, пересекаются в одной точке Эта точка называется ортоцентром треугольника.

 

Высоты остроугольного треугольника расположены строго внутри треугольника.

Соответственно, точка пересечения высот также находится внутри треугольника.

В прямоугольном треугольнике две высоты совпадают со сторонами. (Это высоты, проведенные из вершин острых углов к катетам).

Высота, проведенная к гипотенузе, лежит внутри треугольника (позднее рассмотрим ее свойства).

AC — высота, проведенная из вершины С к стороне AB.

AB — высота, проведенная из вершины B к стороне AC.

AK — высота, проведенная из вершины прямого угла А к гипотенузе ВС.

Высоты прямоугольного треугольника пересекаются в вершине прямого угла (А — ортоцентр).

В тупоугольном треугольника внутри треугольника лежит только одна высота — та, которая проведена из вершины тупого угла.

Две другие высоты лежат вне треугольника и опущены к продолжению сторон треугольника (к прямым, содержащим стороны треугольника).

  AK — высота, проведенная к стороне BC.

BF — высота, проведенная к продолжению стороны АС.

CD — высота, проведенная к продолжению стороны AB.

 

Точка пересечения высот тупоугольного треугольника также находится вне треугольника:

 

H — ортоцентр треугольника ABC.