Биссектриса треугольника |

Биссектриса треугольника

Биссектриса треугольника, в отличие от биссектрисы угла, является отрезком, а не лучом.

Определение

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне.

bissektrisa treugolnika

Таким образом, биссектриса треугольника является частью биссектрисы угла треугольника (луча), которая находится внутри треугольника.

bissektrisyi treugolnika

Все три биссектрисы треугольника пересекаются в одной точке.

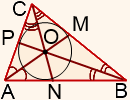
tochka peresecheniya bissektris treugolnika

Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности.

Свойство биссектрисы треугольника

Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам:

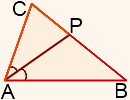
svoystvo bissetrisyi

$\frac{{AC}}{{CP}} = \frac{{AB}}{{BP}}$

Более подробно о свойстве биссектрисы мы поговорим позже.

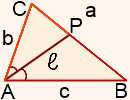
dlina bissektrisyi treugolnika Длина биссектрисы

1) Длина биссектрисы треугольника через длины его сторон.

Если ввести обозначения

$BC = a,AC = b,$

$AB = c,AP = l,$

длина биссектрисы треугольника АВС, проведенная из вершины А, может быть найдена через длины сторон по формуле

$l = \frac{1}{{b + c}}\sqrt {b \cdot c(b + c + a)(b + c - a)} .$

2) Длина биссектрисы треугольника через длины сторон и пропорциональные отрезки.

$AP = \sqrt {AC \cdot AB - CP \cdot BP}$

Если ввести обозначения

$CP = {b_1},BP = {c_1},$

формула длины биссектрисы примет вид:

$l = \sqrt {bc - {b_1}{c_1}}$

3) Длина биссектрисы треугольника через длины сторон и угол между ними:

$AP = \frac{{2 \cdot AC \cdot AB \cdot \cos \angle CAP}}{{AC + AB}}.$

Если ввести обозначение ∠CAB=α, формула примет вид:

$l = \frac{{2bc \cdot \cos \frac{\alpha }{2}}}{{b + c}}.$

One Comment

Чернышова Алиса:

12.02.2016 в 20:50

Спасибо! Эта информация помогла мне при составлении доклада!

Ответить

Добавить комментарий Отменить ответ