Чему равна сумма внешних углов треугольника

Вопрос о том, чему равна сумма внешних углов треугольника, требует уточнения формулировки. Всего у треугольника есть шесть внешних углов — по два при каждой вершине.

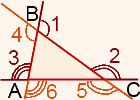Углы каждой пары равны между собой  (как вертикальные):

∠1=∠4,  ∠2=∠5,  ∠3=∠6.

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Поэтому ∠1=∠А+∠С,  ∠2=∠А+∠В, ∠3=∠В+∠С.

Отсюда сумма внешних углов треугольника, взятых по одному при каждой вершине, равна

∠1+∠2+∠3=∠А+∠С+∠А+∠В+∠В+∠С=2(∠А+∠В+∠С).

Так как сумма углов треугольника равна 180º, то ∠А+∠В+∠С=180º. Значит, ∠1+∠2+∠3=2∙180º=360º.

Когда задают вопрос: «Чему равна сумма внешних углов треугольника?», чаще всего имеют в виду именно сумму углов, взятых по одному при каждой вершине. Поэтому следует уточнить формулировку — нужно найти сумму углов, взятых по одному при каждой вершине или сумму всех внешних углов. Сумма всех шести внешних углов, соответственно, в два раза больше: ∠1+∠2+∠3+∠4+∠5+∠6=2(∠1+∠2+∠3)=720º.