Что такое перпендикуляр к прямой? Как построить перпендикуляр к прямой? Сколько перпендикуляров можно провести из точки к прямой? Что такое наклонная? Что называется проекцией наклонной? Об этом — ниже.
Определение.
Перпендикуляр, опущенный из точки A на прямую a — это отрезок, лежащий на прямой, перпендикулярной прямой a, один конец которого — точка A, второй — точка пересечения этих двух прямых.
Как построить перпендикуляр к прямой?

На рисунке 1 изображены прямая a и точка A, не лежащая на прямой a.
Чтобы построить перпендикуляр, воспользуемся угольником.

Угольник располагаем так,
чтобы одна сторона прямого угла проходила вдоль прямой a,
а вторая — через точку A.
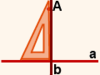
Если провести через точку A вдоль стороны угольника прямую,
то получим прямую b, перпендикулярную данной прямой a.
Нам нужно построить перпендикуляр, то есть отрезок — часть этой прямой.

Соединим точку A с точкой на пересечении прямых a и b
(назовем вторую точку B).
Отрезок AB — перпендикуляр, проведенный из точки A к прямой a.
Точка B называется основанием перпендикуляра.
Расстояние от точки до прямой измеряется длиной перпендикуляра.
Расстояние от точки A до прямой a (рисунок 4) равно длине отрезка AB.
Из данной точки к данной прямой можно провести только один перпендикуляр.
Любой другой отрезок, который соединяет точку A с точкой на прямой a, называется наклонной.
Определение.
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.
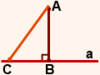
На рисунке 5 AC — наклонная, проведенная из точки A к прямой a.
Точка C называется основанием наклонной AC.
Определение.
Отрезок, который соединяет основание перпендикуляра с основанием данной наклонной, называется проекцией этой наклонной на прямую.
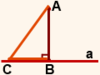
На рисунке 6 BC — проекция наклонной AC на прямую a.
Перпендикуляр часто встречается при решении задач, связанных с треугольниками. В частности, определение высоты треугольника опирается на перпендикуляр.
В следующий раз рассмотрим свойства перпендикуляра и наклонной.
