Тангенс 30 градусов

Найдем тангенс угла 30 градусов с помощью определения тангенса в прямоугольном треугольнике.

Утверждение.

$tg{30^o} = \frac{{\sqrt 3 }}{3}$

Доказательство:

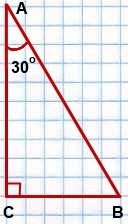tangens 30 Рассмотрим прямоугольный треугольник, один из острых углов которого равен 30 градусам:

∠C=90º, ∠A=35º.

Так как катет, лежащий против угла в 30º, равен половине гипотенузы, то

$BC = \frac{1}{2}AB.$

Пусть

$BC = a, \Rightarrow AB = 2a.$

По теореме Пифагора,

$A{B^2} = A{C^2} + B{C^2}$

${(2a)^2} = A{C^2} + {a^2}$

$A{C^2} = 4{a^2} - {a^2} = 3{a^2}$

$AC = \sqrt {3{a^2}} = a\sqrt 3 .$

По определению тангенса острого угла в прямоугольном треугольнике,

$tg\angle A = \frac{{BC}}{{AC}},$

отсюда,

$tg{30^o} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }}.$

Иррациональность в знаменателе оставлять не принято. Умножаем и числитель, и знаменатель дроби на квадратный корень из трех:

$tg{30^o} = \frac{{1 \cdot \sqrt 3 }}{{\sqrt 3 \cdot \sqrt 3 }} = \frac{{\sqrt 3 }}{3}.$

Что и требовалось доказать.

Переведем угол 30 градусов в радианы:

${30^o} = \frac{\pi }{6}$

Значит, тангенс пи на 6 равен

$tg\frac{\pi }{6} = \frac{{\sqrt 3 }}{3}.$