Что такое окружность, вписанная в треугольник? Какие у вписанной окружности свойства?
Определение.
Окружность называется вписанной в треугольник, если она касается всех его сторон.
Общие точки окружности и треугольника называются точками касания.
 Запись окр. (O; r) читают: «Окружность с центром в точке O и радиусом r».
Запись окр. (O; r) читают: «Окружность с центром в точке O и радиусом r».
На рисунке окр. (O; r) — вписанная в треугольник ABC.
M, K, F- точки касания.
Свойства вписанной в треугольник окружности.

1) Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника.
AO, BO, CO — биссектрисы треугольника ABC.
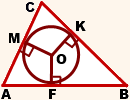
2) Отрезки соединяющие центр вписанной окружности с точками касания, перпендикулярны сторонам треугольника (как радиусы, проведенные в точку касания):
![]()
![]()
![]()

3) Вписанная в треугольник окружность делит стороны треугольника на 3 пары равных отрезков.
![]()
![]()
![]()
(как отрезки касательных, проведенные из одной точки).
