Равные хорды

Выясним, какими свойствами обладают равные хорды и равные дуги.

Утверждение 1.1

Равные хорды равноудалены от центра окружности.

Дано: окр. (O;R), AB и CD — хорды,

AB=CD, OF⊥AB, OK⊥CD

Доказать: OF=OK

Доказательство:

Соединим центр окружности с концами хорд.

I. Рассмотрим треугольники AOB и COD.

1) AB=CD (по условию)

2) OA=OB=OC=OD (как радиусы).

Следовательно, ∆AOB = ∆COD (по трём сторонам).

Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.

II. Рассмотрим прямоугольные треугольники AOF и COK.

1) AO=CO=R

2) ∠A=∠C (по доказанному).

Следовательно,  ∆AOF=∆COK (по гипотенузе и острому углу).

Из равенства треугольников следует равенство соответствующих сторон: OF=OK.

Что и требовалось доказать.

Утверждение 1.2

Если хорды равноудалены от центра окружности, то они равны.

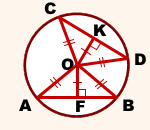Дано: окр. (O;R), AB и CD — хорды,

OF⊥AB, OK⊥CD,

OF=OK

Доказать:  AB=CD

Доказательство:

Соединим центр окружности с концами хорд.

I. Рассмотрим прямоугольные треугольники OKD и OFB.

1)OF=OK (по условию)

2)OD=OB (как радиусы).

Следовательно, ΔOKD=ΔOFB (по катету и гипотенузе).

Из равенства треугольников следует равенство соответствующих сторон:

KD=FB.

II. Рассмотрим треугольники AOB и COD.

Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.

По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.

Что и требовалось доказать.

Утверждение 2.1

Равные хорды стягивают равные дуги.

 

Дано: окр. (O;R), AB и CD — хорды, AB=CD,

Доказать: ∪AB=∪CD

Доказательство:

Соединим центр окружности с концами хорд.

Рассмотрим треугольники AOB и COD

1) AB=CD (по условию)

2) OA=OB=OC=OD (как радиусы).

Следовательно, ∆AOB = ∆COD (по трём сторонам).

Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.

Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD

Что и требовалось доказать.

Утверждение 2.2

Хорды, стягивающие равны дуги, равны.

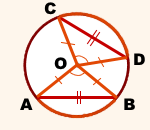Дано: окр. (O;R), AB и CD — хорды,

∪AB=∪CD

Доказать: AB=CD

Доказательство:

Соединим центр окружности с концами хорд.

Рассмотрим треугольники AOB и COD

Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.

∪AB=∠AOB, ∪CD=∠COD.

Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.

Следовательно, ΔAOB=ΔCOD (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: AB=CD.

Что и требовалось доказать.