Расстояние от центра окружности до хорды

Рассмотрим, как найти расстояние от центра окружности до хорды.

Расстояние от точки до прямой измеряется длиной перпендикуляра,  опущенного из этой точки на данную прямую. Значит, расстояние от центра окружности до хорды равно длине перпендикуляра, проведённого из центра окружности к этой хорде.

 

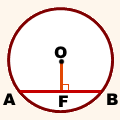
Например, расстояние от точки O — центра окружности — до хорды AB  равно длине перпендикуляра OF:

   

Задача.

Отрезки AB и CD являются хордами окружности. Найти расстояние от центра окружности до хорды CD, если AB=24, CD=10,  а расстояние от центра окружности до хорды AB равно 5.

Дано: окружность (O; R), AB и CD — хорды,

   

AB=24, CD=10, OF=5

Найти: OK

Решение:

1) Соединим центр окружности с концами хорд.

2) Треугольники AOB и COD — равнобедренные с основаниями AB и CD (AO=BO=CO=DO как радиусы).

Значит, их высоты OF и OK являются также медианами. Следовательно,

   

3) Рассмотрим треугольник AOF, где ∠AFO=90 º.

По теореме Пифагора

   

   

4) Рассмотрим треугольник COK, где ∠CKO=90 º.

По теореме Пифагора

   

   

Ответ: 12.