Теорема (свойство высоты равнобедренного треугольника)
Высота равнобедренного треугольника, проведенная к основанию, является его медианой и биссектрисой.

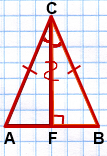
Дано: ∆ ABC,
AC=BC,
CF — высота.
Доказать:
CF — медиана и биссектриса.
Доказательство:

Рассмотрим треугольники
ACF и BCF.
1) AC=BC (по условию
(как боковые стороны равнобедренного треугольника))
2) сторона CF — общая
∠AFC=∠BFC=90º (как смежные)
∠A=∠B (как углы при основании равнобедренного треугольника)
Сумма углов треугольника равна 180º.
Если из 180º вычесть сумму равных углов, то получим равные углы:
![]()
 Таким образом, имеем:
Таким образом, имеем:
3) ∠ACF=∠BCF.
Следовательно,
- CF — биссектриса треугольника ABC
- ∆ ACF=∆ BCF ( по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон: AF=BF.
Поэтому CF является также медианой треугольника ABC.
Что и требовалось доказать.

Ну вобщем доказательство этой теоремы не совсем корректно. Потому что предполагает предварительное введение признаков равенства треугольников, включая признаки равенства прямоугольных треугольников. Потому что тут напрямую можно воспользоваться равенством тр. AFC и тр. FCB по общему катету CF и гипотенузам AC и BC… Но дело в том, что введение этих признаков требует доказательства ряда теорем и свойств и по курсу геометрии предполагается после этой теоремы. Поэтому по логике такое доказательство не совсем уместно… Мы приходим к логическому противоречию. И потому требуется другое доказательство, не требующее использования признаков равенства треугольников. Это же доказательство ещё хуже, поскольку тут потребовали ещё и равенства углов противолежащих равным сторонам. (Это отдельная теорема, которая так же излагается после). Хотя этот недостаток легко устраняется… Но доказательство получается довольно таки запутанным. Вначале надо провести биссектрису(как обычно и доказывается эта теорема) и доказать равенство этих углов. Но если выбрать такой путь, то гораздо проще провести сразу биссектрису(не высоту!!!) и доказать всю теорему. А потом ввести следствия и доказать эту на основании уже доказанной скажем методом от противного. Так обычно и излагается этот материал. Но если мы хотим доказать все свойства через высоту, то надо придумать что-то другое…