Утверждение
Если в треугольник вписан параллелограмм таким образом, что один угол у них общий, а три другие вершины параллелограмма лежат на сторонах треугольника, то параллелограмм отсекает два треугольника, подобных данному.
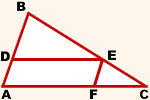 Дано: ∆ ABC, ADEF — параллелограмм,
Дано: ∆ ABC, ADEF — параллелограмм,
D∈AB, E∈BC, F∈AC.
Доказать:
![]()
![]()
 Доказательство:
Доказательство:
1) Рассмотрим треугольники DBE и ABC.
У них:
- ∠B — общий,
- ∠BDE=∠BAC (как соответственные при DE ∥ AC и секущей AB).
Следовательно,
![]()
2) Аналогично, по двум углам подобны треугольники FEC и ABC.
У них:
- ∠C — общий,
- ∠FEC=∠ABC (как соответственные при AB ∥ FE и секущей BC).
3) Кроме того, треугольники DBE и FEC также подобны (по двум углам либо как подобные одному и тому же треугольнику).
Что и требовалось доказать.
Задача
 Дано: ∆ ABC, ADEF- параллелограмм,
Дано: ∆ ABC, ADEF- параллелограмм,
AC=30 см, AB=20 см,
![]()
Найти: DE, EF.
Решение:
По доказанному,
![]()
![]()
![]()
(здесь k — коэффициент пропорциональности), откуда
![]()
Площади подобных треугольников относятся как квадраты их соответствующих сторон, следовательно,
![]()
![]()
![]()
![]()
Ответ: 12 см, 8 см.
