Свойство секущих

Теорема

(Свойство секущих)

Для каждой из секущих, проведённых из одной точки, произведение длины секущей на длину её внешней части есть величина постоянная.

Дано: окружность (O; R), AB и AC — секущие,

AB∩окр. (O; R)=F, AC∩окр. (O; R)=K

Доказать:

AB ∙ AF=AC ∙ AK

Доказательство:

I способ

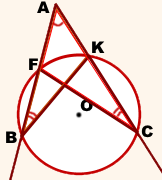Рассмотрим треугольники ABK и ACF.

∠A — общий угол;

∠ABK=∠ACF (как вписанные углы, опирающиеся на одну дугу FK).

Следовательно, треугольники ABK и ACF подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

По основному свойству пропорции:

   

Что и требовалось доказать.

II способ

1) Проведём отрезки FK и BC.

2) Так как четырёхугольник BFKC — вписанный в окружность, то сумма его противолежащих углов равна 180º:

∠BCK+∠BFK=180º. Следовательно, ∠BFK=180º-∠BCK.

3) ∠AFK+∠BFK=180º (как смежные). Отсюда,

∠AFK=180º-∠BFK=180º-(180º-∠BCK)=180º-180º+∠BCK=∠BCK,

то есть ∠AFK=∠BCK.

4) Рассмотрим треугольники ABC и AKF.

У них ∠ACB=∠AFK (так как ∠AFK=∠BCK по доказанному), ∠A — общий угол. Следовательно, треугольники ABC и AKF — подобны (по двум углам).

Отсюда,

   

Что и требовалось доказать.

При решении задач будем использовать свойство секущих, а также запомним полученные в ходе доказательства теоремы факты о подобии треугольников, образованных секущими. Причем подобие треугольников ABC и AKF можно доказывать как приведённым выше способом, так и опираясь на свойство секущих.