Признак равенства по катету и острому углу

Теорема 1

(Признак равенства прямоугольных треугольников по катету и прилежащему острому углу)

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Дано:

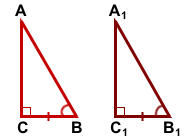
ΔABC, ΔA₁B₁C₁,

∠C=90°, ∠C₁=90°,

BC=B₁C₁,  ∠B=∠B₁

Доказать: ΔABC= ΔA₁B₁C₁

Доказательство:

По условию, в треугольниках ABC и ΔA₁B₁C₁:

1) BC=B₁C₁;

2)∠C=∠C₁;

3) ∠B=∠B₁.

Следовательно, ΔABC= ΔA₁B₁C₁(по стороне и двум прилежащим к ней углам).

Что и требовалось доказать.

Теорема 2

(Признак равенства прямоугольных треугольников по катету и противолежащему углу)

Если катет и противолежащий ему угол одного прямоугольного треугольника соответственно равны катету и противолежащему ему углу другого прямоугольного треугольника, то такие треугольники равны.

Дано:

ΔABC, ΔA₁B₁C₁,

∠C=90°, ∠C₁=90°, BC=B₁C₁,

∠A=∠A₁

Доказать: ΔABC= ΔA₁B₁C₁

Доказательство:

По условию, в треугольниках ABC и ΔA₁B₁C₁:

1) BC=B₁C₁;

2)∠C=∠C₁;

3)Так как сумма острых углов прямоугольного треугольника равна 90°,

то есть ∠ B=∠ B₁.

Следовательно, ΔABC= ΔA₁B₁C₁(по стороне и двум прилежащим к ней углам).

Что и требовалось доказать.