Расстояние от точки пересечения диагоналей ромба |

Как найти расстояние от точки пересечения диагоналей ромба до одной из его сторон? Каков его геометрический смысл?

Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к данной прямой. Точка пересечения диагоналей ромба является также центром вписанной в него окружности. Расстояние от центра до любой точки окружности равно её радиусу. Следовательно, расстояние от точки пересечения диагоналей ромба до одной из её сторон равно радиусу вписанной в ромб окружности.

Радиус вписанной в ромб окружности равен половине высоты ромба. Также его можно найти по формуле

$r = \frac{S}{p},$

где S — площадь, p — полупериметр ромба.

Задача 1.

Расстояние от точки пересечения диагоналей ромба до одной из её сторон равно r, а одна из диагоналей равна d. Найти углы ромба.

Решение:

rasstoyanie-ot-tochki-peresecheniya-diagonalej-romba Пусть в ромбе ABCD AC∩BD=O,

$OK \bot AD.$

AC=d, OK=r.

По свойствам ромба, его диагонали взаимно перпендикулярны, в точке пересечения делятся пополам и делят углы ромба пополам.

В прямоугольном треугольнике AOK

$AO = \frac{1}{2}AC, \Rightarrow AO = \frac{d}{2},$

$\angle KAO = \frac{1}{2}\angle BAD.$

По определению синуса,

$\sin \angle KAO = \frac{{OK}}{{AO}},\[\sin \angle KAO = \frac{{OK}}{{AO}}, \Rightarrow \sin \angle KAO = \frac{r}{{\frac{d}{2}}} = \frac{{2r}}{d},$

$\angle KAO = \arcsin (\frac{{2r}}{d}).$

∠ABC+∠BAD=180º (как внутренние односторонние при AD∥BC и секущей AB). Следовательно,

$\angle ABC = {180^o} - \angle KAO = {180^o} - \arcsin (\frac{{2r}}{d}).$

В частности, если расстояние от точки пересечения диагоналей ромба до одной из сторон в 4 раза меньше длины диагонали (AC=4∙OK, то есть d=4r), то

$\sin \angle KAO = \frac{{2r}}{{4r}} = \frac{1}{2}.$

Поскольку угол между диагональю и стороной ромба не может быть тупым (иначе угол ромба должен быть больше 180º), то ∠KAO=30º,

∠BAD=2∙30º=60º,

∠ABC=180º-∠BAD=180º-60º=120º.

Ответ: 60º, 120º.

Задача 2

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 5, а одна из диагоналей ромба равна 20. Найти углы ромба.

rasstoyanie-ot-tochki-peresecheniya Дано: ABCD — ромб, AC∩BD=O,

$OF \bot AB.$

AC=20, OF=5.

Найти: углы ромба

Решение:

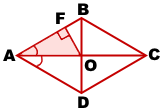
rasstoyanie-ot-tochki-peresecheniya-diagonalej

Рассмотрим треугольник AOF, ∠AFO=90º, OF=5 (по условию).

$AO = \frac{1}{2}AC$

(по свойству ромба),

$AO = \frac{1}{2}\cdot20 = 10, \Rightarrow FO = \frac{1}{2} \cdot AO.$

Так как катет FO равен половине гипотенузы AO, то он лежит напротив угла в 30º: ∠OAF=30º.

Так как диагонали ромба являются биссектрисами его углов, то ∠BAD=2∙∠OAF=60º.

∠ABC+∠BAD=180º (как внутренние односторонние при AD∥BC и секущей AB). Следовательно, ∠ABC=180º-∠BAD=120º.

Ответ: 60º, 120º.

Расстояние от точки пересечения диагоналей ромба

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики