Радиус описанной окружности

Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.

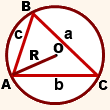
Радиус описанной окружности для произвольного треугольника

Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):

radius opisannoy okruzhnosti

$R = \frac{{abc}}{{4S}}$

$R = \frac{a}{{2\sin \alpha }} = \frac{b}{{2\sin \beta }} = \frac{c}{{2\sin \gamma }},$

где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.

Центр описанной окружности лежит:

radius opisannoy okruzhnosti tupougolnogo treugolnika

у остроугольного треугольника — внутри треугольника;

у прямоугольного — на середине гипотенузы;

у тупоугольного — вне треугольника, напротив тупого угла.

Радиус описанной окружности для прямоугольного треугольника

radius opisannoy okruzhnosti pryamougolnogo treugolnika

Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:

$R = \frac{c}{2}$

Окружность, описанная около многоугольника

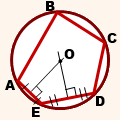
radius opisannoy okruzhnosti mnogougolnika

Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.

Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.

Радиус окружности, описанной около правильного многоугольника

Формула радиуса описанной окружности для правильного многоугольника

$R = \frac{a}{{2\sin \frac{{{{180}^o}}}{n}}}$