Окружность, описанная около правильного треугольника |

Окружность, описанная около правильного треугольника, обладает всеми свойствами описанной около произвольного треугольника окружности и, кроме того, имеет свои собственные свойства.

1) Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров к его сторонам.

Поскольку в равностороннем треугольнике медианы, высоты и биссектрисы совпадают, центр описанной около правильного треугольника окружности лежит в точке пересечения его медиан, высот и биссектрис.

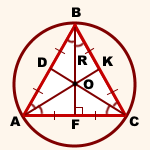okruzhnost-opisannaya-okolo-pravilnogo-treugolnika Например, в правильном треугольнике ABC AB=BC=AC=a

точка O — центр описанной окружности.

AK, BF и CD — медианы, высоты и биссектрисы треугольника ABC.

$AK \cap BF = O,$

$AK \cap CD = O.$

2) Расстояние от центра описанной окружности до вершин треугольника равно радиусу. Так как центр описанной около равностороннего треугольника окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус описанной окружности составляет две трети от длины медианы:

$BO = \frac{2}{3}BF,$

$R = \frac{2}{3} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}.$

Таким образом, формула радиуса описанной около правильного треугольника окружности —

$R = \frac{{a\sqrt 3 }}{3}$

И обратно, сторона равностороннего треугольника через радиус описанной окружности —

$a = \frac{{3R}}{{\sqrt 3 }} = R\sqrt 3 .$

3) Формула для нахождения площади правильного треугольника по его стороне —

$S = \frac{{{a^2}\sqrt 3 }}{4}.$

Отсюда можем найти площадь через радиус описанной окружности:

$S = \frac{{a^2 \sqrt 3 }}{4} = \frac{{(R\sqrt 3 )^2 \cdot \sqrt 3 }}{4} = \frac{{R^2 \cdot 3\sqrt 3 }}{4}.$

Таким образом, формула площади площади правильного треугольника через радиус описанной окружности —

$S = \frac{{3\sqrt 3 \cdot R^2 }}{4}.$

4) Центр описанной около правильного треугольника окружности совпадает с центром вписанной в него окружности.

5) Радиус описанной около равностороннего треугольника окружности в два раза больше радиуса вписанной окружности:

$\left. \begin{array}{l} BO = R,OF = r\\ BO = \frac{2}{3}BF,OF = \frac{1}{3}BF \end{array} \right\} \Rightarrow R = 2r.$

Окружность, описанная около правильного треугольника

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики