Утверждение.
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
![]()
(d1, d2 — диагонали четырёхугольника, φ — угол между ними).
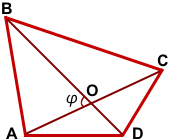 Дано: ABCD — выпуклый четырёхугольник,
Дано: ABCD — выпуклый четырёхугольник,
AC∩BD=O, AC=d1, BD=d2, ∠AOB=φ
Доказать:
![]()
Доказательство:
Диагонали выпуклого четырёхугольника ABCD делят его на 4 треугольника.
Площадь каждого из треугольников равна половине произведения его сторон на синус угла между ними:
![]()
![]()
![]()
![]()
∠BOC=180°-∠AOB=180°-φ (как смежные).
∠COD=∠AOB=φ,
∠AOD=∠BOC=180°-φ (как вертикальные).
sin (180°-φ)=sin φ.
Отсюда
![]()
![]()
![]()
![]()
Таким образом,
![]()
![]()
![]()
![]()
![]()
![]()
Что и требовалось доказать.

Спасибо всем!
Большое спасибо! Очень хороший сайт.