Угол между высотами треугольника

Как найти угол между высотами треугольника? Зависит ли величина угла от вида треугольника?

Утверждение.

Один из углов, образованный высотами треугольника, проведёнными из двух его вершин, равен углу при третьей вершине.

Другой угол равен сумме углов треугольника, из вершин которых проведены высоты.

Доказательство:

1 способ

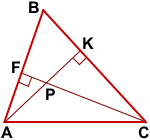
Рассмотрим остроугольный треугольник ABC.

Пусть AK и CF — его высоты.

Тогда ∠BFC=∠BKA=90°.

Так как сумма углов четырёхугольника равна 360°, то в 4-угольнике BKPF

∠BFP+∠FPK+∠BKP+∠FBK=360°,

откуда ∠FPK+∠FBK=180° и ∠FPK=180°-∠FBK.

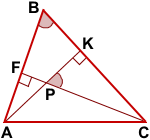∠FPK+∠KPC=180° (как смежные).

∠KPC=180°-∠FPK=180°-(180° -∠FBK)=∠FBK.

Так как сумма углов треугольника равна 180°,

∠BAC+∠FBK+∠ACB=180°,

∠FBK=180°-(∠BAC+∠ACB),

∠FPK=180°-∠FBK=180° -(180° -(∠BAC+∠ACB))=∠BAC+∠ACB.

2 способ

Прямоугольные треугольники BCF и PKC подобны по общему острому углу C. Следовательно, ∠KPC=∠FBC.

 

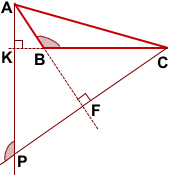
Если треугольник ABC — тупоугольный, рассуждения и вывод аналогичны.

Утверждение верно и для прямоугольного треугольника.

То есть для любого треугольника ABC один из углов между высотами, проведёнными из вершин A и C, равен углу B, другой — сумме углов A и C.

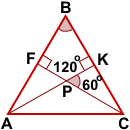В частности, один угол между высотами равностороннего треугольника равен 60°, другой — 120°:

∠KPC=60°,

∠FPK=120°.