Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.
Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0.
Расстояние от точки (xo;yo) до прямой ax+by+c=0 определяется по формуле
![]()
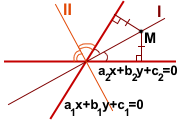 По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.
По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0, находится от этих прямых на одинаковом расстоянии, то есть
![]()
Это равенство можно записать в виде
![]()
Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.
Пример.
Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.
Решение:
В формулу уравнения биссектрис подставляем данные прямых:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: 3x+3y-23=0; 21x-21y-37=0.
